常见模型方法·费马点模型【模型专题】

费马点模型

【模型分析】

费马点是指平面内到三角形三个顶点距离之和最小的点，这个最小的距离叫做费马距离．

若三角形内有一个内角大于等于120°，则此钝角的顶点就是到三个顶点距离之和最小的点．若三角形的内角均小于120°，那么三角形的费马点与各顶点的连线三等分费马点所在的周角；

1、若三角形有一个内角大于等于120°，则此钝角的顶点即为该三角形的费马点

如图在△ABC中，∠BAC≥120°，求证：点A为△ABC的费马点

证明：

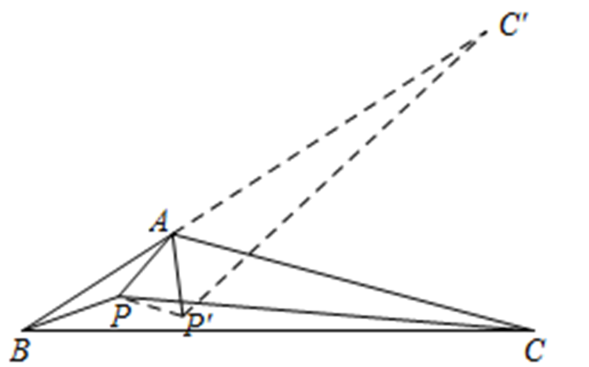
如图，在△ABC内有一点P延长BA至C，使得AC＝AC，作∠CAP＝ ∠CAP，并且使得AP＝AP，连结PP

则△APC≌△APC，PC＝PC

因为∠BAC≥120°

所以∠PAP′＝∠CAC≤60

所以在等腰△PAP中，AP≥PP′

所以PA＋PB＋PC≥PP′＋PB＋PC＞BC＝AB＋AC

所以点A为△ABC的费马点

2、若三角形的内角均小于120°，则以三角形的任意两边向外作等边三角形，两个等边三角形外接圆在三角形内的交点即为该三角形的费马点．

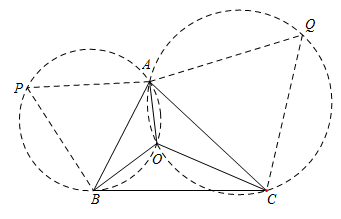
如图，在△ABC中三个内角均小于120°，分别以AB、AC为边向外作等边三角形，两个等边三角形的外接圆在△ABC内的交点为O，求证：点O为△ABC的费马点

证明：在△ABC内部任意取一点O，；连接OA、OB、OC

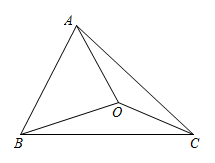
将△AOC绕着点A逆时针旋转60°，得到△AO′D连接OO′则O′D＝OC

所以△AOO′为等边三角形，OO′＝AO

所以OA＋OC＋OB＝OO′＋OB＋O′D

则当点B、O、O′、D四点共线时，OA＋OB＋OC最小

此时AB、AC为边向外作等边三角形，两个等边三角形的外接圆在△ABC内的交点即为点O

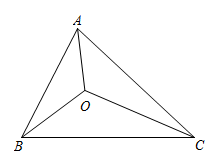
3、如图，在△ABC中，若∠BAC、∠ABC、∠ACB均小于120°，O为费马点，则有∠AOB＝∠BOC＝∠COA＝120°，所以三角形的费马点也叫三角形的等角中心

类型一 线段的系数都相同求线段的和的情况（费马点）

考法1：费马点在三角形中运用

例1

【变式】

【变式】

考法2：费马点在四边形中运用

例2

【变式】

【变式】

考法3：费马点在二次函数中运用

例3

【变式】

类型二 线段的系数都不相同求线段的和的情况（加权费马点）

【模型通解】

第一步，选定固定不变线段；

第二步，对剩余线段进行缩小或者放大．

如：保持BP不变，x_AP＋y_BP＋z_CP＝$y(\frac{x}{y}AP+BP+\frac{z}{y}CP)$，如图所示，B、P、P₂、A₂四点共线时，取得最小值．

例4：

例5：

【变式】（1）

【变式】

【变式】

【变式】

【变式】