专题34 晶体结构及相关计算

【题型一】晶体的结构分析
【典例分析】
(2022·山东省等级考)
【提分秘籍】
1.典型的晶体结构
(1)金属晶体的四种堆积方式
堆积名称 | 面心立方最密堆积 | 体心立方堆积 | 六方最密堆积 | 简单立方堆积 |
晶胞结构 | 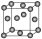 |  | 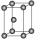 | 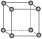 |
堆积类型 | A1型或铜型 | A2型或钾型 | A3型或镁型 | Po型 |
堆积方式 | …ABCABC… | …ABAB… | ||
 | 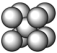 | 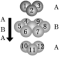 | 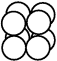 | |
配位数 | 12 | 8 | 12 | 6 |
空间利用率 | 74% | 68% | 74% | 52% |
典型代表 | Cu、Ag、Au | Na、K、Fe | Mg、Zn、Ti | Po |
(2)典型离子晶体的空间构型
类型 | NaCl型 | CsCl型 | 立方ZnS型 | CaF2型 |
图示 | 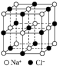 | 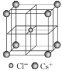 | 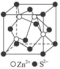 | 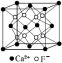 |
结构特点 | 1/8晶胞为简单立方结构 | 体心立方结构 | 间隔排列的4个小立方体的体心各有1个Zn2+ | 8个小立方体的体心各有1个F- |
配位数 | 6 | 8 | 4 | Ca2+:8 F-:4 |
空隙形状 | 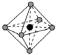 | 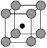 | 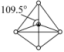 |   |
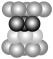
(3)常见分子晶体和共价晶体的晶胞
晶胞 | 二氧化碳 | 金刚石 | 碳化硅 | 二氧化硅 |
图示 | 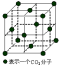 | 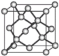 | 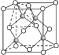 | 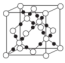 |
结构特点 | 面心立方 | 同ZnS | 将金刚石中内部的4个碳原子换成硅原子 | 将晶体硅中每个硅硅键中间插入1个氧原子 |
配位数 | 12 | 4 | 6 | Si:4;O:2 |
2.晶胞中微粒数目的计算方法——均摊法
(1)立方体晶胞
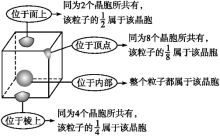
(2)其他晶胞
①顶点上微粒:被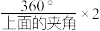 个晶胞共用
个晶胞共用
②侧棱上微粒:被顶点一半的晶胞共用
晶胞 | 正六棱柱 | 正三棱柱 |
示意图 | 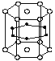 | 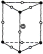 |
顶点上微粒 | 6 | 12 |
侧棱上微粒 | 3 | 6 |
③上下棱上微粒:被4个晶胞共用
④面点上微粒:被2个晶胞共用
⑤内部的微粒:被1个晶胞独用
【变式演练】
【题型二】晶胞密度的计算
【典例分析】
(2022·湖南省等级考)
【提分秘籍】
1.密度公式:ρ=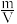 =
=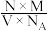
2.晶胞的体积
几何体 | 图示 | 计算公式 |
立方体 | 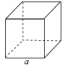 | V=a3 |
长方体 | 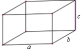 | V=abc |
正三棱柱 | 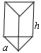 | V=  a2hsin60°= a2hsin60°=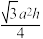 |
正六棱柱 | 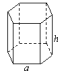 | V=6×  a2hsin60°= a2hsin60°=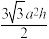 |
正四面体 | 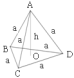 | S= 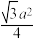 ,h= ,h=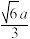 ,V= ,V=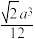 |
平行六面体 | 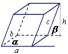 | S=ab×sinα h=csinβ V=abcsinαsinβ |
3.单位换算
(1)1pm=10-12m=10-10cm
(2)1nm=10-9m=10-7cm
(3)1μm=10-6m=10-4cm
【变式演练】
【题型三】微粒间距的计算
【典例分析】
(2022·广东省等级考)
【提分秘籍】
1.晶体中某些几何体中的数量关系(晶胞参数为a)
(1)立方体晶胞:边长和体对角线及面对角线的关系
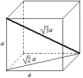
(2)面心立方晶胞:相邻的两个面心间的距离和边长的关系
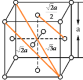
(3)立方体套正四面体晶胞:最近的黑球和白球间的距离
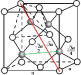
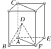
(4)正四面体中各量的关系
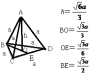
①直角三角形BEC中:(BC)2=(CE)2+(BE)2
②BO= BE,OE=
BE,OE= BE
BE
③直角三角形AOB中:(AB)2=(BO)2+(AO)2
2.某些晶胞中微粒间的最短距离(晶胞参数为a)
类型 | 图示 | 最近距离 |
NaCl型 |  | 阴阳离子间:  a a同号离子间: 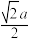 |
CsCl型 |  | 阴阳离子间: 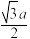 同号离子间:a |
立方ZnS型 |  | 阴阳离子间: 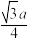 同号离子间: 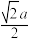 |
CaF2型 |  | 阴阳离子间: 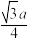 同号离子间: 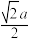 |
二氧化碳型 |  | 微粒间最近距离: 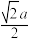 |
金刚石型 |  | 微粒间最近距离: 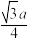 |
【变式演练】
【题型四】空间利用率计算
【典例分析】
(2021·全国乙卷)
【提分秘籍】
1.空间利用率= ×100%=
×100%=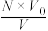 ×100%
×100%
(1)原子的体积:V V0=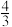 πr3(r为原子半径)
πr3(r为原子半径)
(2)晶胞体积
①根据晶胞参数计算:①V=Sh;②V锥= Sh
Sh
②根据密度计算:V=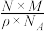
2.金属晶体原子半径(r)和晶胞参数(a)的关系
(1)面心立方:面对角线上的三个原子相切:4r=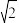 a
a
(2)体心立方:体对角线上的三个原子相切:4r=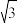 a
a
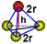
(3)简单立方:侧面上的原子两两相切:2r=1a
(4)六方最密:正四面体相邻原子两两相切:2r=1a
3.晶体摩尔体积的计算:Vm=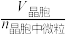 =
=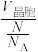 =
=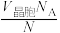
【变式演练】



