实战高考·二轮热点题型归纳与变式演练·专题08 动量问题综合-2023年高考物理毕业班二轮热点题型归纳与变式演练（全国通用）

专题08：动量问题综合

考点1 冲量和动量定理

考点2 动量和动量守恒定律

考点3 动量定理与动量守恒定律的综合

考点4 动力学、动量和能量观点的综合应用

考点5 三种观点解决力学问题

考点1 冲量和动量定理

（1）恒力的冲量可应用I＝Ft直接求解，变力的冲量优先考虑应用动量定理求解，合外力的冲量可利用I＝F_合·t或I_合＝Δp求解。

（2）动量定理的表达式是矢量式，在一维情况下，各个矢量必须选取统一的正方向。

1．应用动量定理解释的两类物理现象

（1）当物体的动量变化量一定时，力的作用时间Δt越短，力F就越大，力的作用时间Δt越长，力F就越小，如玻璃杯掉在水泥地上易碎，而掉在沙地上不易碎。

（2）当作用力F一定时，力的作用时间Δt越长，动量变化量Δp越大，力的作用时间Δt越短，动量变化量Δp越小。

2．应用动量定理解题的一般步骤

（1）确定研究对象。中学阶段的动量定理问题，其研究对象一般仅限于单个物体。

（2）对物体进行受力分析。可以先求每个力的冲量，再求各力冲量的矢量和；或先求合力，再求其冲量。

（3）抓住过程的初、末状态，选好正方向，确定各动量和冲量的正、负号。

（4）根据动量定理列方程，如有必要还需要其他补充方程，最后代入数据求解。对过程较复杂的运动，可分段用动量定理，也可整个过程用动量定理。

（1）判断动量是否守恒时，要注意所选取的系统，注意区别系统内力与外力。系统不受外力或所受合外力为零时，系统动量守恒。

（2）动量守恒具有矢量性，若系统在某个方向上合力为零，则系统在该方向上满足动量守恒定律。

（3）动量守恒表达式：m₁v₁＋m₂v₂＝m₁v′₁＋m₂v′₂或p＝p′或Δp＝0。

考点2 动量和动量守恒定律

（1）判断动量是否守恒时，要注意所选取的系统，注意区别系统内力与外力。系统不受外力或所受合外力为零时，系统动量守恒。

（2）动量守恒具有矢量性，若系统在某个方向上合力为零，则系统在该方向上满足动量守恒定律。

（3）动量守恒表达式：m₁v₁＋m₂v₂＝m₁v′₁＋m₂v′₂或p＝p′或Δp＝0。

[2021·甘肃天水期末]

[2021·浙江卷]

[2021·安徽师大附中检测]

考点3 动量定理与动量守恒定律的综合

（1）动量定理与动量守恒定律都是矢量方程，应用时要规定正方向，同时要关注速度、速度变化量、动量及动量变化量的矢量性。

（2）动量定理关注力和力的作用时间，而动量守恒定律要关注系统内相互作用过程。

几种常见模型的特点及规律

模型	特点及满足的规律
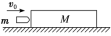	子弹打入木块若未穿出，系统动量守恒，能量守恒，即mv0＝（m＋M）v，Q热＝fL相对＝mv02－（M＋m）v2若子弹穿出木块，有mv0＝mv1＋Mv2，Q热＝fL相对＝mv02－mv12－Mv22
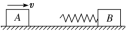	（1）弹簧处于最长（最短）状态时两物体速度相等，弹性势能最大，系统满足动量守恒、机械能守恒，即 m1v0＝（m1＋m2）v共，m1v02＝（m1＋m2）v共2＋Epm。 （2）弹簧处于原长时弹性势能为零，系统满足动量守恒、机械能守恒，即m1v0＝m1v1＋m2v2，m1v02＝m1v12＋m2v22
模型	表面粗糙、质量为M的木板，放在光滑的水平地面上，质量为m的小木块以初速度v0滑上木板，若木块未滑离木板，当木块与木板相对静止时，二者的共同速度为v，木块相对木板的位移为d，木板相对地面的路程为s，木块和木板间的摩擦力为f。这类问题类似于子弹打木块模型中子弹未射出的情况，则有mv0＝（M＋m）v， f·d＝mv02－（M＋m）v2＝mv02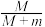。 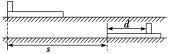若木块滑离木板，设滑离木板时，木块的速度为v1，木板的速度为v2木板长为l，则根据动量守恒定律有mv0＝mv1＋Mv2，摩擦力和相对路程的乘积等于系统动能的减少量，有 f·l＝mv02－mv12－Mv22。

[2021·广安高三检测]

[2021·山东滨州市重点中学高考模拟]

考点4 动力学、动量和能量观点的综合应用

1．动量与能量的综合问题，常取材“滑块—滑板”模型、“传送带”模型、“弹簧—物块”模型等，设置多个情景、多个过程，考查力学三大观点的综合应用。要成功解答此类“情景、过程综合”的考题，就要善于在把握物理过程渐变规律的同时，洞察过程的临界情景，结合题给条件（往往是不确定条件），进行求解（注意结合实际情况分类讨论）。

2．“三大观点”的选取原则

（1）当涉及功、能和位移时，一般选用动能定理、机械能守恒定律、功能关系或能量守恒定律解题，题目中出现相对位移时，应优先选择能量守恒定律。

（2）当涉及多个物体及时间时，一般考虑动量定理、动量守恒定律。

（3）当涉及细节并要求分析力时，一般选择牛顿运动定律，对某一时刻的问题进行求解。

（4）复杂的问题一般需综合应用能量的观点、运动与力的观点解题。

[2021·浙江卷]

考点5 三种观点解决力学问题

1．解动力学问题的三个基本观点

2．力的瞬时作用和力的空间积累作用

3．动量观点和能量观点的比较

[2021广东惠州模拟]

【易错01】动能、动量、动量变化量的比较

	动能	动量	动量变化量
定义	物体由于运动而具有的能量	物体的质量和速度的乘积	物体末动量与初动量的矢量差
定义式	Ek＝mv2	p＝mv	Δp＝p′－p
标矢性	标量	矢量	矢量
特点	状态量	状态量	过程量
关联 方程	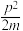Ek＝，Ek＝pv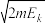，p＝，p＝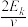
联系	（1）都是相对量，与参考系的选取有关，通常选取地面为参考系 （2）若物体的动能发生变化，则动量一定也发生变化；但动量发生变化时动能不一定发生变化

【易错02】动量定理及其应用理解有误

1．动量定理的研究对象可以是单个物体，也可以是物体系统。对物体系统，只需分析系统受的外力，不必考虑系统内力。系统内力的作用不改变整个系统的总动量。

2．用牛顿第二定律和运动学公式能求解恒力作用下的匀变速直线运动的间题，凡不涉及加速度和位移的，用动量定理也能求解，且较为简便。

但是，动量定理不仅适用于恒定的力，也适用于随时间变化的力。对于变力，动量定理中的F应当理解为变力在作用时间内的平均值。

3．用动量定理解释的现象一般可分为两类：一类是物体的动量变化一定，此时力的作用时间越短，力就越大；时间越长，力就越小。另一类是作用力一定，此时力的作用时间越长，动量变化越大；力的作用时间越短，动量变化越小。分析问题时，要把哪个量一定哪个量变化搞清楚。

4．应用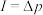求变力的冲量：如果物体受到变力作用，则不直接用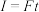求变力的冲量，这时可以求出该力作用下的物体动量的变化，等效代换变力的冲量I。

5．应用求恒力作用下的曲线运动中物体动量的变化：曲线运动中物体速度方向时刻在改变，求动量变化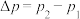需要应用矢量运算方法，比较复杂，如果作用力是恒力，可以求恒力的冲量，等效代换动量的变化。

【易错03】“三类”模型问题中动量守恒定律及其应用理解有误

1．“子弹打木块”模型

（1）“木块”放置在光滑的水平面上

①运动性质：“子弹”对地在滑动摩擦力作用下做匀减速直线运动；“木块”在滑动摩擦力作用下做匀加速直线运动。

②处理方法：通常由于“子弹”和“木块”的相互作用时间极短，内力远大于外力，可认为在这一过程中动量守恒。把“子弹”和“木块”看成一个系统：a.系统水平方向动量守恒；b.系统的机械能不守恒；c.对“木块”和“子弹”分别应用动能定理。

（2）“木块”固定在水平面上

①运动性质：“子弹”对地在滑动摩擦力作用下做匀减速直线运动；“木块”静止不动。

②处理方法：对“子弹”应用动能定理或牛顿第二定律。

2．“反冲”和“爆炸”模型

（1）反冲

①定义：当物体的一部分以一定的速度离开物体时，剩余部分将获得一个反向冲量，这种现象叫反冲运动。

②特点：系统内各物体间的相互作用的内力远大于系统受到的外力。实例：发射炮弹、发射火箭等。

③规律：遵从动量守恒定律。

（2）爆炸问题

爆炸与碰撞类似，物体间的相互作用时间很短，作用力很大，且远大于系统所受的外力，所以系统动量守恒。如爆竹爆炸等。

3．“人船模型”问题

（1）模型介绍

两个原来静止的物体发生相互作用时，若所受外力的矢量和为零，则动量守恒。在相互作用的过程中，任一时刻两物体的速度大小之比等于质量的反比。这样的问题即为“人船模型”问题。

（2）模型特点

①两物体满足动量守恒定律：m₁v₁－m₂v₂＝0。

②运动特点：人动船动，人静船静，人快船快，人慢船慢，人左船右；人船位移比等于它们质量的反比；人船平均速度（瞬时速度）比等于它们质量的反比，即＝＝。

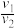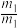③应用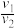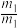＝＝时要注意：v₁、v₂和x₁、x₂一般都是相对地面而言的。

[2022·山东青岛高三期末]

[2022·安徽合肥一模]

[2022·湖南卷·T7]

[2022·湖南卷·T4]

[2022·山东卷·T2]

[2022·全国乙卷·T20]

[2021·广西钦州综测]

[2021·江西崇义中学模拟]

[2021·四川遂宁零诊]

[2021·广西桂林市、百色市和崇左市第三次联考]

[2021·温州高三模拟]

[2021·河南省中原名校第六次模拟]

[2021·云南省腾冲市质检]

[2020·陕西省西安一中一模]

[2021·四川宜宾第四中学开学考试]

[2021·河南郑州高三期末]

[2021·山东潍坊高三一模]

[2021·内蒙古自治区高三一模]

[2021·山东省高考模拟]

[2021·长春市第一一五中学高三月考]

[2021·四川省德阳市第三中学高考模拟]

[2021·北京高三学业考试]