2023年高考物理一轮复习提升核心素养·6.3“碰撞类”模型问题-2023年高考物理一轮复习提升核心素养

6.3“碰撞类”模型问题

一、碰撞的特点和分类

1．碰撞的特点

（1）时间特点：碰撞现象中，相互作用的时间极短，相对物体运动的全过程可忽略不计。

（2）相互作用力特点：在碰撞过程中，系统的内力远大于外力，所以动量守恒。

2．碰撞的分类

（1）弹性碰撞：系统动量守恒，机械能守恒。

（2）非弹性碰撞：系统动量守恒，机械能减少，损失的机械能转化为内能。

（3）完全非弹性碰撞：系统动量守恒，碰撞后合为一体或具有相同的速度，机械能损失最大。

3．爆炸：一种特殊的“碰撞”

特点1：系统动量守恒。

特点2：系统动能增加。

二、弹性正碰模型

1．“一动碰一静”模型

2．如果两个相互作用的物体，满足动量守恒的条件，且相互作用过程初、末状态的总机械能不变，广义上也可以看成弹性正碰。

三、碰撞可能性分析

判断碰撞过程是否存在的依据

1．满足动量守恒：p₁＋p₂＝p₁′＋p₂′。

2．满足动能不增加原理：E_k1＋E_k2≥E_k1′＋E_k2′。

3．速度要符合情景

（1）如果碰前两物体同向运动，则后面物体的速度必大于前面物体的速度，即v_后＞v_前，否则无法实现碰撞。碰撞后，原来在前的物体的速度一定增大，且原来在前的物体的速度大于或等于原来在后的物体的速度v_前′≥v_后′。

（2）如果碰前两物体是相向运动，则碰后两物体的运动方向不可能都不改变，除非两物体碰撞后速度均为零。若碰后沿同向运动，则前面物体的速度大于或等于后面物体的速度，即v_前≥v_后。

“滑块—弹簧”模型

1．模型图示

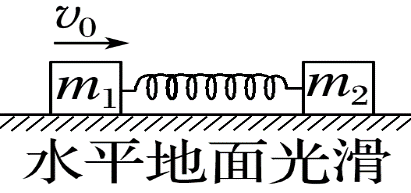
2．模型特点

（1）动量守恒：两个物体与弹簧相互作用的过程中，若系统所受外力的矢量和为零，则系统动量守恒。

（2）机械能守恒：系统所受的外力为零或除弹簧弹力以外的内力不做功，系统机械能守恒。

（3）弹簧处于最长（最短）状态时两物体速度相等，弹性势能最大，系统动能通常最小（相当于完全非弹性碰撞，两物体减少的动能转化为弹簧的弹性势能）。

（4）弹簧恢复原长时，弹性势能为零，系统动能最大（相当于刚完成弹性碰撞）．

“滑块—斜（曲）面”模型

1．模型图示

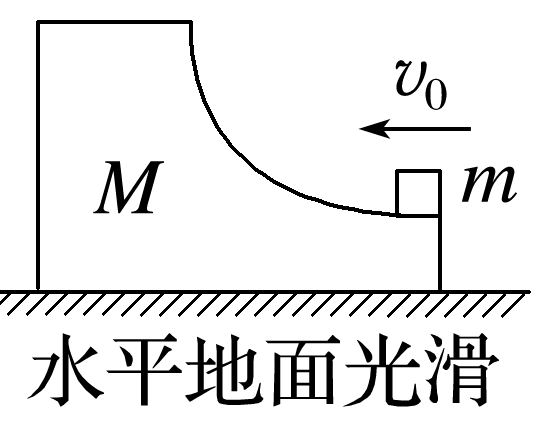
2．模型特点

（1）上升到最大高度：m与M具有共同水平速度v_共，此时m的竖直速度v_y＝0．系统水平方向动量守恒，mv₀＝（M＋m）v_共；系统机械能守恒，$\frac{1}{2}$mv₀²＝$\frac{1}{2}$（M＋m）v_共²＋mgh，其中h为滑块上升的最大高度，不一定等于弧形轨道的高度（相当于完全非弹性碰撞，系统减少的动能转化为m的重力势能）。

（2）返回最低点：m与M分离点。水平方向动量守恒，mv₀＝mv₁＋Mv₂；系统机械能守恒，$\frac{1}{2}$mv₀²＝$\frac{1}{2}$mv₁²＋$\frac{1}{2}$Mv₂²（相当于完成了弹性碰撞）。

“物体与物体”正碰模型

1．碰撞遵守的规律

（1）动量守恒，即p₁＋p₂＝p₁′＋p₂′。

（2）动能不增加，即E_k1＋E_k2≥E_k1′＋E_k2′或$\frac{p_1^2}{2m_1}$＋$\frac{p_2^2}{2m_2}$≥$\frac{p_1^{\prime 2}}{2m_1}$＋$\frac{p_2^{12}}{2m_2}$。

（3）速度要符合情景：如果碰前两物体同向运动，则后面物体的速度必大于前面物体的速度，即v_后>v_前，否则无法实现碰撞。碰撞后，原来在前面的物体的速度一定增大，且原来在前面的物体的速度大于或等于原来在后面的物体的速度，即v_前′≥v_后′，否则碰撞没有结束。如果碰前两物体相向运动，则碰后两物体的运动方向不可能都不改变，除非两物体碰撞后速度均为零。

2．碰撞模型类型

（1）弹性碰撞

两球发生弹性碰撞时应满足动量守恒和机械能守恒。

以质量为m₁、速度为v₁的小球与质量为m₂的静止小球发生正面弹性碰撞为例，有

m₁v₁＝m₁v₁′＋m₂v₂′

$\frac{1}{2}$m₁v${}_1^2$＝$\frac{1}{2}$m₁v₁′²＋$\frac{1}{2}$m₂v₂′²

解得v₁′＝$\frac{(m_1-m_2)v_1}{m_1+m_2}$，v₂′＝$\frac{2m_1{v}_1}{m_1+m_2}$。

结论：

①当两球质量相等时，v₁′＝0，v₂′＝v₁，两球碰撞后交换了速度。

②当质量大的球碰质量小的球时，v₁′>0，v₂′>0，碰撞后两球都沿速度v₁的方向运动。

③当质量小的球碰质量大的球时，v₁′<0，v₂′>0，碰撞后质量小的球被反弹回来。

④撞前相对速度与撞后相对速度大小相等。

（2）完全非弹性碰撞

①撞后共速。

②有动能损失，且损失最多。

“滑块—木板”碰撞模型

模型 图示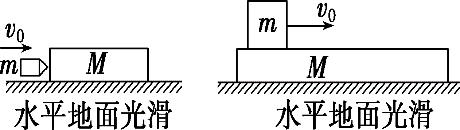
模型 特点	（1）若子弹未射穿木块或滑块未从木板上滑下，当两者速度相等时木块或木板的速度最大，两者的相对位移（子弹为射入木块的深度）取得极值（完全非弹性碰撞拓展模型） （2）系统的动量守恒，但机械能不守恒，摩擦力与两者相对位移的乘积等于系统减少的机械能 （3）根据能量守恒，系统损失的动能ΔEk＝$\frac{M}{m+M}$Ek0，可以看出，子弹（或滑块）的质量越小，木块（或木板）的质量越大，动能损失越多 （4）该类问题既可以从动量、能量角度求解，相当于非弹性碰撞拓展模型，也可以从力和运动的角度借助图示求解