模型4 相互独立事件的辨析问题模型

【模板探究】
母题呈现 | 模板引入 |
设事件  与事件 与事件 满足: 满足: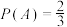 , ,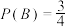 , , ,则下列说法正确的是( ) ,则下列说法正确的是( )A.事件  与事件 与事件 不是相互独立事件 不是相互独立事件B.事件  与事件 与事件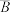 不是相互独立事件 不是相互独立事件C.事件  与事件 与事件 是相互独立事件 是相互独立事件D.事件  与事件 与事件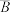 不是相互独立事件 不是相互独立事件 | 本模板解决的是“判断所给出的事件是否为相互独立事件”的问题. |
解析:因为  ,所以事件 ,所以事件 和事件 和事件 是相互独立事件,故C正确, 是相互独立事件,故C正确,则  与 与 , , 与 与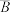 和 和 和 和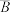 都是相互独立事件. 都是相互独立事件.故选:C | 第一步 分析题意,分别求出 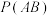 , ,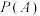 , ,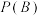 第二步 验证 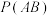 是否等于 是否等于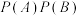 第三步 得出结论 |
【必备知识】
1相互独立事件的定义
相互独立事件指的是两个或多个事件之间不会相互影响,即一个事件的发生与否对另一个事件的发生概率没有影响.数学上,如果事件A和事件B满足P(A∩B) = P(A)P(B),则称事件A和B是相互独立的.
2相互独立事件的性质
如果事件A和事件B是相互独立的,那么它们的补事件也是相互独立的.
如果事件A和事件B是相互独立的,那么它们的交集事件、并集事件、倍数事件,以及经过加、减、乘、除运算后的事件都是相互独立的.
更一般地,如果有n(n≥2)个事件A1, A2, ..., An,如果对于其中任意2个、任意3个、...、任意n个事件的积事件的概率,都等于各个事件概率之积,则称这些事件是相互独立的.
3 判断方法
检查事件之间是否有重叠部分,如果两个事件之间有重叠,则它们不是完全独立的.
检查事件之间是否有先后顺序,如果一个事件的发生与否会影响另一个事件的发生概率,则这两个事件不是相互独立的.
检查是否满足乘法原理,即两个事件的概率相乘是否等于它们同时发生的概率,如果满足,则这两个事件是相互独立的.
需要注意的是,满足加法原理的事件(即两个事件的概率之和等于它们任意一个事件发生的概率加上另一个事件发生的概率)不是相互独立的.
4互斥事件与相互独立事件的辨析
互斥事件与相互独立事件都是描述两个事件间的关系,但互斥事件强调不可能同时发生,相互独立事件强调一个事件是否发生对另一个事件发生的概率没有影响.互斥的两个事件可以相互独立,相互独立的两个事件也可以互斥.
互斥事件的概率公式: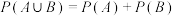 .
.
相互独立事件的概率公式:
【解决方法】
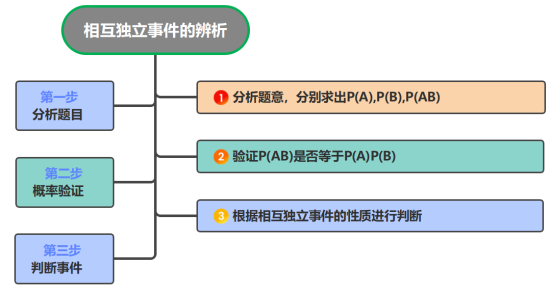

【典例1】已知样本空间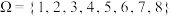 ,事件
,事件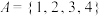 ,事件
,事件 ,事件
,事件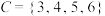 ,则下列选项错误的是( )
,则下列选项错误的是( )
A. 与
与 独立 B.
独立 B. 与
与 独立
独立
C. 与
与 独立 D.
独立 D.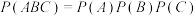
【答案】D
【套用模板】
第一步:分析题意,分别求出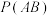 ,
,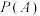 ,
,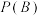
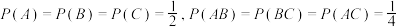 ,
,
第二步:验证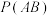 是否等于
是否等于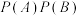
有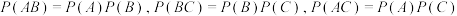 ,
,
但 ,
,
第三步:得出结论
故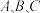 两两独立,ABC正确;D错误.
两两独立,ABC正确;D错误.
故选:D.
【典例2】有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回地随机取两次,每次取1个球.甲表示事件“第一次取出的球的数字是4”,乙表示事件“第二次取出的球的数字是5”,丙表示事件“两次取出的球的数字之和是6”,丁表示事件“两次取出的球的数字之和是7”,则( )
A.甲与乙互斥 B.丙发生的概率为 C.甲与丁相互独立 D.乙与丙相互独立
C.甲与丁相互独立 D.乙与丙相互独立
【答案】C
【套用模板】
第一步:分析题意,分别求出甲,乙,丙,丁发生概率
由题意可知,两点数和为6的所有可能为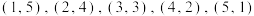 ,
,
两点数和为7的所有可能为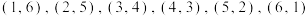 ,
,
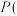 甲
甲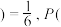 乙
乙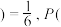 丙
丙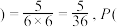 丁
丁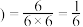 ,
,
第二步:分析事件关系,并运用相互独立事件的概率公式进行验证
 (甲丁)
(甲丁)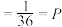 (甲)
(甲) (丁),
(丁), (乙丙)
(乙丙)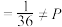 (乙)
(乙) (丙)
(丙)
第三步:得出结论
综上所述,对于A选项,甲与乙可以同时发生,故选项A错误;
对于B选项,由上可知错误,故选项B错误;
对于C选项,甲与丁相互独立,故选项C正确;
对于D选项,乙与丙相互独立不成立,故选项D错误.
故选:C.
【典例3】在一次考试中有一道4个选项的双选题,其中A和B是正确选项,C和D是错误选项,甲,乙两名同学都完全不会这道题目,只能在4个选项中随机选取两个选项.设事件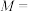 “甲、乙两人所选选项恰有一个相同”,事件
“甲、乙两人所选选项恰有一个相同”,事件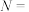 “甲、乙两人所选选项完全不同”,事件
“甲、乙两人所选选项完全不同”,事件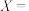 “甲、乙两人所选选项完全相同”,事件
“甲、乙两人所选选项完全相同”,事件 “甲、乙两人均未选择B选项”,则( )
“甲、乙两人均未选择B选项”,则( )
A.事件M与事件N相互独立 B.事件M与事件Y互为对立事件
C.事件X与事件Y相互独立 D.事件N与事件Y为互斥事件
【答案】D
【套用模板】
第一步:分析题意,分别求出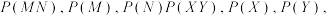
依题意甲、乙两人所选选项有如下情形:
一个选项相同,②两个选项相同,③两个选项不相同,
所以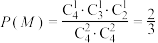 ,
,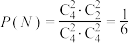 ,
,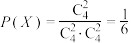 ,
,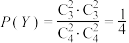 ,
,
因为事件 与事件
与事件 互斥,所以
互斥,所以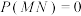 ,
,
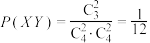
第二步:验证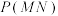
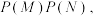
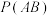
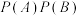
因为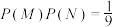 ,
,
所以事件 与事件
与事件 不相互独立,故A错误;
不相互独立,故A错误;
由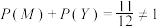 ,所以事件
,所以事件 与事件
与事件 不互为对立事件,故B错误;
不互为对立事件,故B错误;
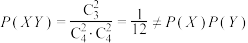 ,故C错误;
,故C错误;
“甲、乙两人所选选项完全不同”与“甲、乙两人均未选择B选项”不能同时发生,事件 与事件
与事件 互斥,故D错误.
互斥,故D错误.
第三步:得出结论
故选:D

(2024福建福州高一期末)
(2024江苏淮安高一期末)
(2024安徽黄山高一期末)
(2024山东烟台高一期末)


