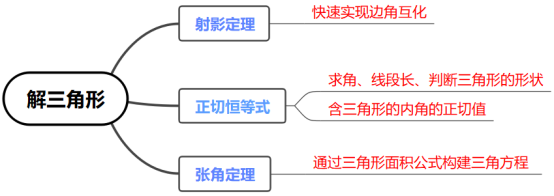
专题20 3个二级结论速解解三角形问题

二级结论1:射影定理
在 中,
中,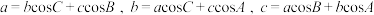 .
.
二级结论2:正切恒等式
若△为斜三角形,则有
二级结论3:张角定理
在 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,若
,若 为
为 上一点(如图),且
上一点(如图),且 ,
,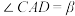 ,则有
,则有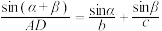 .
.


【典例1】 的内角
的内角 的对边分别为
的对边分别为 ,若
,若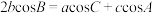 ,则
,则 .
.
【大招指引】利用射影定理将等式化为2bcosB=b即可求解.
【解析】∵在△ABC中,acosC+ccosA=b,
∴条件等式变为2bcosB=b,∴cosB= .
.
又0<B<π,∴B= .
.
【题后反思】本题也可以利用正弦定理进行求解:
由2bcosB=acosC+ccosA及正弦定理,得2sinBcosB=sinAcosC+sinCcosA.
∴2sinBcosB=sin(A+C).
又A+B+C=π,∴A+C=π-B.∴2sinBcosB=sin(π-B)=sinB.
又sinB≠0,∴cosB= .∴B=
.∴B= .
.
【温馨提醒】解三角形问题,多为边和角的求值问题,这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系,从而达到解决问题的目的;射影定理是正弦定理、余弦定理的一个重要结推论,应用射影定理快速实现边角互化,进而解决求边、角及与三角形有关的最值等问题.
【举一反三】
【典例2】在锐角三角形 中,
中, ,则
,则 的最小值是( ).
的最小值是( ).
A.3 B.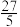 C.
C.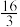 D.12
D.12
【大招指引】化简 可得
可得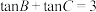 ,将
,将 化成
化成 ,即可根据
,即可根据 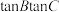 的范围求解
的范围求解
【解析】∵ ,∴
,∴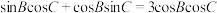 ,
,
∴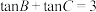 ,
,
∴
 ,
,
∵ ,当且仅当
,当且仅当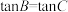 时取等号,
时取等号,
∴ .
.
故选:B.
【题后反思】本题也可以按以下方法进行求解:
∵ ,∴
,∴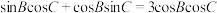 ,
,
∴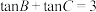 ,
,
∴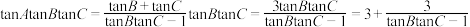 ,
,
∵ ,当且仅当
,当且仅当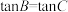 时取等号,
时取等号,
∴ .
.
故选:B.
【温馨提醒】正切恒等式常用于求角、线段长、判断三角形的形状、证明不等式以及求含有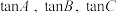 式子的最值等题型.
式子的最值等题型.
【举一反三】
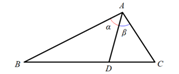
【典例3】在△ABC中,角A、B、C所对的边分别为 、b、c,已知点D在BC边上,AD⊥AC,sin∠BAC
、b、c,已知点D在BC边上,AD⊥AC,sin∠BAC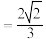 , AB
, AB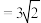 ,AD=3,则CD是多少?
,AD=3,则CD是多少?
【大招指引】先利用同角三角函数基本关系求出cos∠BAC,再利用张角定理进行求解.
【解析】如图:

∵sin∠BAC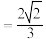
∴cos∠BAC
由张角定理得: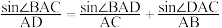
即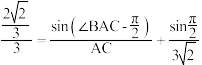
即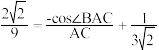
即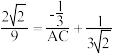
解得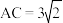
∴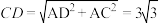
【题后反思】因为本题条件中出现 ,所以联想到张角定理得到
,所以联想到张角定理得到
使用张角定理得到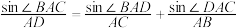 ,这是解决本题的关键.
,这是解决本题的关键.
【温馨提醒】张角定理的本质是通过三角形面积公式构建三角方程,如本题中利用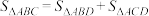 得到
得到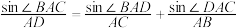 .
.
【举一反三】



