专题3 数列的实际应用和综合问题




【必备知识】
1.公式法
(1)等差数列{an}的前n项和为: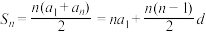 ,推导方法为倒序相加法.
,推导方法为倒序相加法.
(2)等比数列{an}的前n项和为: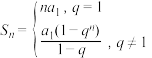 ,推导方法为乘公比与错位相减法.
,推导方法为乘公比与错位相减法.
(3)一些常见的数列的前n项和:
①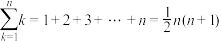 ;
;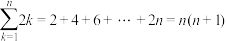 .
.
②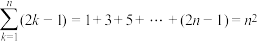 ;
;
③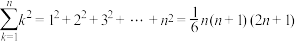 ;
;
④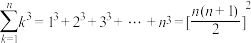 .
.
2.几种数列求和的常用方法
(1)分组转化求和法:一个数列的通项公式是由若干个等差或等比或可求和的数列组成的,则求和时可用分组求和法,分别求和后相加减.
(2)裂项相消法:把数列的通项拆成两项之差,在求和时中间的一些项可以相互抵消,从而求得前n项和.
(3)错位相减法:如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的,那么求这个数列的前n项和即可用错位相减法求解.
(4)倒序相加法:如果一个数列 与首末两端等“距离”的两项的和相等或等于同一个常数,那么求这个数列的前n项和即可用倒序相加法求解.
与首末两端等“距离”的两项的和相等或等于同一个常数,那么求这个数列的前n项和即可用倒序相加法求解.
【必备技能】
常见的裂项技巧:
①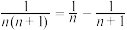 ;
;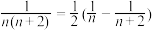 ;
;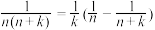 ;
;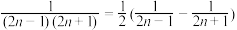 ;
;
②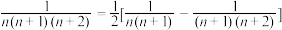 ;
;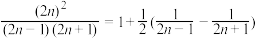 ;
;
③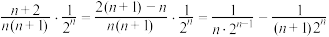 ;
;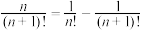 ;
;
④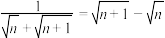 ;
;
⑤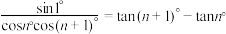 ;
;
常见放缩公式: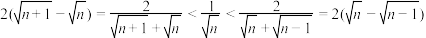 .
.
【考向总览】
考向一:等差数列、等比数列的综合运算(★★★★)
考向二:数列与不等式的交汇(★★★)
考向三:数列与函数的交汇(★★★)
【考向归类】
考向一:等差数列、等比数列的综合运算
【典例1-1】
(2022·辽宁辽阳·统考二模)
【典例1-2】
(2022下·江苏南通·高一统考期中)
【备考提醒】
数列的综合问题常将等差、等比数列结合,两者相互联系、相互转化,解答这类问题的方法:寻找通项公式,利用性质进行转化.
【举一反三】
考向二:数列与不等式的交汇
【典例2-1】
(2023·陕西咸阳·武功县普集高级中学校考模拟预测)
【典例2-2】
(2023·河南驻马店·统考二模)
【备考提醒】
数列与不等式的综合问题及求解策略
①判断数列问题的一些不等关系,可以利用数列的单调性比较大小或借助数列对应的函数的单调性比较大小.
②以数列为载体,考查不等式恒成立的问题,此类问题可转化为函数的最值.
③考查与数列有关的不等式证明问题,此类问题一般采用放缩法进行证明,有时也可通过构造函数进行证明.
【举一反三】
(2023下·辽宁铁岭·高二校联考期中)
(2023上·福建莆田·高二莆田华侨中学校考期中)
考向三:数列与函数的交汇
【典例3-1】
(2023·全国·模拟预测)
【典例3-2】
(2023·江苏连云港·统考一模)
【备考提醒】
数列与函数交汇问题的主要类型及求解策略
①已知函数条件,解决数列问题,此类问题一般利用函数的性质、图象研究数列问题.
②已知数列条件,解决函数问题,解决此类问题一般要利用数列的通项公式、前n项和公式、求和方法等对式子化简变形.
【举一反三】
(2023·四川成都·校联考一模)
(2023·江苏泰州·统考一模)

【必备知识】
1.等差数列的有关概念
(1)等差数列的定义
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,通常用字母 表示,定义表达式为
表示,定义表达式为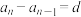 (常数)
(常数)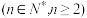 .
.
(2)等差中项
若三个数 ,
, ,
, 成等差数列,则
成等差数列,则 叫做
叫做 与
与 的等差中项,且有
的等差中项,且有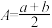 .
.
2.等差数列的有关公式
(1)等差数列的通项公式
如果等差数列 的首项为
的首项为 ,公差为
,公差为 ,那么它的通项公式是
,那么它的通项公式是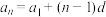 .
.
(2)等差数列的前 项和公式
项和公式
设等差数列 的公差为
的公差为 ,其前
,其前 项和
项和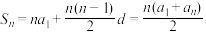 .
.
3.等比数列的有关概念
(1)定义:如果一个数列从第2项起,每一项与它的前一项的比等于同一常数(不为零),那么这个数列就叫做等比数列.这个常数叫做等比数列的公比,通常用字母 表示,定义的表达式为
表示,定义的表达式为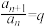 .
.
(2)等比中项:如果 ,
, ,
, 成等比数列,那么
成等比数列,那么 叫做
叫做 与
与 的等比中项.
的等比中项.
即 是
是 与
与 的等比中项 ⇔
的等比中项 ⇔ ,
, ,
, 成等比数列 ⇒
成等比数列 ⇒  .
.
4.等比数列的有关公式
(1)等比数列的通项公式
设等比数列 的首项为
的首项为 ,公比为
,公比为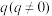 ,则它的通项公式.
,则它的通项公式.
推广形式: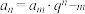
(2)等比数列的前n项和公式
等比数列 的公比为
的公比为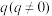 ,其前
,其前 项和为
项和为 ,则当
,则当 时,
时,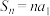 ;当
;当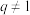 时,
时,
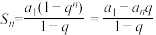 .
.
【必备技能】
数列在数学文化与实际问题中的应用
纵观近几年高考,数列以数学文化为背景的问题,层出不穷,让人耳目一新.同时它也使考生们受困于背景陌生,阅读受阻,使思路无法打开.本节通过对典型高考问题的剖析、数学文化的介绍、及精选模拟题的求解,让考生提升审题能力,增加对数学文化的认识,进而加深对数学文化理解,发展数学核心素养.
【考向总览】
考向一:数列的实际应用(★★★)
【考向归类】
考向一:数列的实际应用
【典例2-1】
【典例2-2】
【举一反三】
(2022下·河北石家庄·高二校联考期中)
(2023·全国·高三专题练习)


