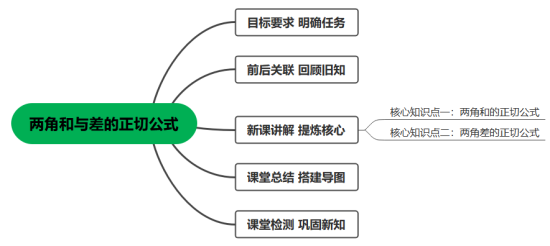
5.5.1课时2 两角和与差的正切公式
【第一课】上好三课,做好三套题,高中数学素养晋级之路

【课标要求】
1.能利用两角和与差的正弦、余弦公式推导出两角和与差的正切公式.
2.能利用两角和与差的正切公式进行化简、求值、证明.
【明确任务】
1.掌握两角和与差的正弦、余弦公式推导出两角和与差的正切公式的方法.【逻辑推理】
2.能熟练利用两角和与差的正切公式进行化简、求值、证明.【数学运算】

1.两角和与差的正弦、余弦公式
sin(α±β)=sinαcosβ±cosαsinβ;
cos(α∓β)=cosαcosβ±sinαsinβ;

核心知识点1: 两角和的正切公式
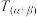 :
: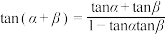 .
.
解读:
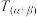 可由
可由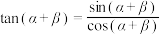 推导;
推导;
公式的结构特征:
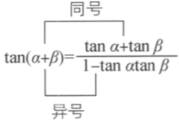
变形结论:
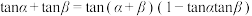 ;
;
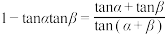
例1.求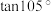 的值.
的值.
【解】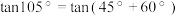
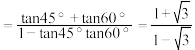
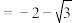 .
.
归纳总结: 若化简的式子中出现了“tan α±tan β”及“tan α·tan β”两个整体,常考虑tan(α±β)的变形公式.
【举一反三】
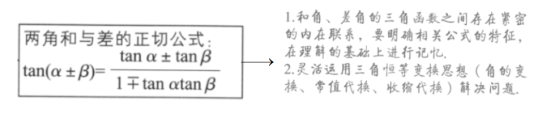
核心知识点2:两角差的正切公式
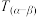 :
: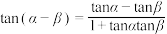 .
.
解读: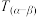 可由
可由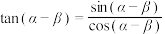 或用
或用 代替
代替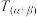 中的
中的 推导.
推导.
公式的结构特征:
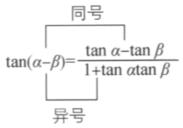
变形结论:
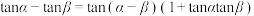 ;
;
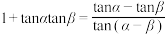 .
.
例2.(2023·全国·高一随堂练习)已知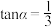 ,
, ,求
,求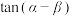 的值.
的值.
【答案】7
【分析】利用差角的正切公式计算即得.
【详解】由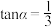 ,
, ,得
,得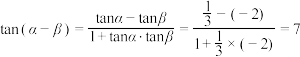 .
.
归纳总结:注意公式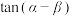 与
与 的区别,公式可以正用、逆用、变形用,根据题意灵活选择.
的区别,公式可以正用、逆用、变形用,根据题意灵活选择.
【举一反三】
【举一反三】(2023上·广东肇庆·高一校考期末)


(2023·河南·信阳高中校联考模拟预测)
(2023下·江苏苏州·高一南京航空航天大学苏州附属中学校考阶段练习)
(2023·上海师大附中月考)
(2024上·湖北·高三统考期末)
(2023下·四川宜宾·高一校考阶段练习)

打开组卷App 获取专属积分,充值下载直接抵现

