专题21 圆锥曲线中的轨迹方程的求法
轨迹方程历年高考中的热门考点，常在解答题中第（1）问出现.本专题主要研究圆锥曲线中关于轨迹方程求法.首先正确理解曲线与方程的概念，会用解析几何的基本思想和坐标法研究几何问题，用方程的观点实现几何问题的代数化解决，并能根据所给条件选择适当的方法求曲线的轨迹方程，常用方法有：直译法、定义法、相关点法、参数（交轨）法、点差法等.
另一方面求轨迹方程是培养学生数形转化的思想、方法以及技巧的极好教材.该内容不仅贯穿于“圆锥曲线”的教学的全过程，而且在建构思想、函数方程思想、化归转化思想等方面均有体现和渗透.
一、热点题型归纳
题型1、直译法
题型2、相关点法
题型3、定义法
题型4、参数法（交轨法）
题型5、点差法
二、最新模考题组练
三、十年高考真题练
【题型1】 直译法
【解题技巧】直译法：若动点运动的条件是一些已知（或通过分析得出）几何量的等量关系，可转化成含x，y的等式，就得到轨迹方程.
知识储备：两点间距离公式，点到直线的距离公式，直线的斜率（向量）公式等.
【典例分析】
例1．（2022·重庆南开中学模拟预测）
例2．（2022·安徽蚌埠·一模）
由例1、2推广：圆锥曲线统一定义（第二定义）：到定点的距离与到定直线的距离的比e是常数的点的轨迹叫做圆锥曲线.当0<e<1时为椭圆：当e=1时为抛物线；当e>1时为双曲线..
例3．（2022·辽宁鞍山·一模）
例4．（2022·江苏·高三期中）
由例3、4推广（圆锥曲线第三定义）：平面内的动点到两定点A和B的斜率之积为e²-1的点的轨迹为椭圆或双曲线.其中点A、B关于原点对称，当0<e²<1时为椭圆，当e²>1时为双曲线.
注意：上述定义有个小瑕疵就是该动点轨迹不包含A、B两点.
【变式演练】
（2022·湖南·长沙模拟预测）
（2022·宁夏·高三期中（理））
（2022·山东潍坊·三模）
【题型2】 相关点法
【解题技巧】
相关点法：若轨迹点P（x ，y）与已知曲线上的动点Q（x0， y0）有关联，则可先列出关于x、y， x0、y0的方程组，利用x、y表示出x0、y0，把x0、y0 代入已知曲线方程便得动点P的轨迹方程.
该方法也可拓展到极坐标系下，按相似处理方式完成.
注：若线段存在倍分关系，一般情况采用直角坐标系下的相关点处理；若存在旋转变换，一般可在极坐标系下进行相关点处理.
知识储备：重心坐标公式；向量的运算公式；极坐标系的相关运算等.
【典例分析】
例1．（2022·福建福州模拟预测）
例2．（2022·黑龙江·哈尔滨模拟预测）
例3．（2022·成都市·高三专题练习）
相关点法也可拓展到极坐标体系下，如例4
例4．（2022·黑龙江·模拟预测）
【变式演练】
（2022·广东·高三专题练习）
（2022·青海·海东模拟预测）
（2022·湖北高考模拟）
【题型3】 定义法
【解题技巧】
定义法：运用解析几何中一些常用定义（圆锥曲线的定义），再从曲线定义出发直接写出轨迹方程.
知识储备：圆：（动点到定点的距离为定值）；椭圆：（动点到两定点距离之和为定值）；双曲线：（动点到两定点距离之差为定值）；抛物线：（动点到定点与到定直线的距离相等）.
【典例分析】
例1．（2022·江苏·高三专题练习）
（2022·贵州·高三开学考试（理））
（2022·安徽·合肥模拟预测（理））
（2022·上海·高三专题练习）
【变式演练】
（2022·湖北·襄阳四中模拟预测）
（2022·内蒙古·三模）
（2021·山东烟台·高三期中）
【题型4】参数法（交轨法）
【解题技巧】
参数法（交轨法）：如果不易直接找出动点的坐标之间的关系，可考虑借助中间变量（参数），把x，y联系起来．其实某种意来说，交轨法也可看作参数法.
【典例分析】
例1．（2022·浙江绍兴·模拟预测）
例2．（2022·福建漳州模拟预测）
例3．（2022·河南洛阳·三模（理））
【变式演练】
（2022·河南·高三课时练习）
（2022·陕西·模拟预测（理））
（2022·成都七中高三模拟）
【题型5】点差法
【解题技巧】
点差法：圆锥曲线中与弦的中点有关的问题一般可用点差法，
基本方法是把弦的两端点A（x1，y1），B（x2，y2）的坐标代入圆锥曲线方程，然而相减，利用平方差公式可得x1+x2， y1+y2， x1-x2， y1-y2 等关系式，由于弦AB的中点P（x， y）的坐标满足2x= x1+x2， 2y= y1+y2且直线AB的斜率为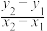
，由此可求得弦AB的中点的轨迹方程.
【典例分析】
例1．（2022·全国·高三课时练习）
例2．（2022·贵州·高三期末）
【变式演练】
（2022·山东·高三专题练习）
（2022·浙江·高三专题练习）
