专题14 数列的通项公式
数列是高中数学的基本板块，是高考数学中的热点和必考点，数列的通项作为数列的灵魂，因此数列的通项公式的求法就备受命题老师亲睐.特别是递推数列的通项问题是高考的热点问题，又是高中数学教学的难点之一.综观近年的高考试题可知，高考数学往往通过考查递推数列来考查学生对数学知识的探究能力.数列大题第一问往往也考察递推公式为主的求通项，这也是复习的重点.本专题就累加法、累乘法、倒数法、待定系数法、定义法等十多种方法逐一进行分析，以便大家熟练掌握.
一、热点题型归纳
题型1. 等差（等比）定义型
题型2. 累加法
题型3. 累乘法
题型4. 倒数法
题型5. 取对数法
题型6. 待定系数法
题型7. 同除以指数幂
题型8. 已知通项公式
与前
项的和
关系求通项问题
题型9. “求和公式换元”型（新数列前n项和型）
题型10. 奇偶讨论型
题型11. 周期数列
二、最新模考题组练
三、十年高考真题练
【题型1】 等差（等比）定义型
【解题技巧】
等差数列判定：①定义法：证an＋1－an＝定值；②等差中项法：即证2an＋1＝an＋an＋2； =
③函数结论法：即an为一次函数或Sn为无常数项的二次函数.
等比数列的判定方法：（1）定义法：证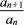
＝q（q≠0的常数）⇔数列{an}是等比数列；
（2）等比中项法：即证a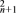
＝an·an＋2（anan＋1an＋2≠0，n∈N*）⇔数列{an}是等比数列．
【典例分析】
（2023·浙江·高三专题练习）
（2023·绵阳市·高三模拟预测）
（2022·陕西西安·高三校联考期中）
【变式演练】
（2023·甘肃·高三阶段练习）
（2022·江苏苏州·高三期中）
（2022·四川·校联考模拟预测）
【题型2】 累加法
【解题技巧】形如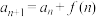
型的递推数列（其中
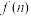是关于的函数）叫累加法.
可构造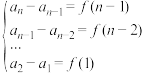
将上述
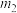个式子两边分别相加，
可得：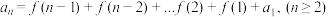
①若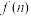是关于的一次函数，累加后可转化为等差数列求和；
② 若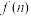是关于的指数函数，累加后可转化为等比数列求和；
③若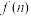是关于的二次函数，累加后可分组求和；
④若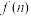是关于的分式函数，累加后可裂项求和．
【典例分析】
（2022·河南·高三专题练习）
（2022·广西·高三专题练习）
【变式演练】
（2022·陕西·模拟预测（理））
（2022·江西赣州·二模（理））
【题型3】累乘法
【解题技巧】形如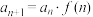
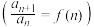型的递推数列（其中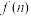是关于的函数）叫累乘法.
可构造：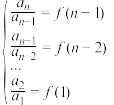
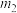将上述个式子两边分别相乘，可得：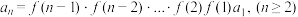
有时若不能直接用，可变形成这种形式，然后用这种方法求解．
【典例分析】
（2022·广西·高三专题练习）
（2022·山西太原·二模（理））
【变式演练】
（2022·浙江浙江·二模）
（2022·成都市·高三专题练习（理））
（2022·河南·模拟预测（理））
【题型4】倒数法
【解题技巧】
1）形如
（
为常数且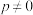
）的递推式：两边同除于
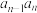，转化为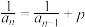
形式，化归为
型求出
的表达式，再求；
2）形如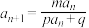
的递推式，也可采用取倒数方法转化成
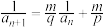形式，化归为型求出的表达式，再求．
【典例分析】
（2023秋·贵州贵阳·高三统考期末）
（2022·江苏南京·模拟预测）
【变式演练】
（2022·山西·怀仁市高三阶段练习）
（2022·全国·高三专题练习）
（2023·湖北高三课时练习）
【题型5】 取对数法
【解题技巧】形如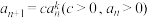
的递推公式，则常常两边取对数转化为等比数列求解．
【典例分析】
（2022·上海市高三期末）
（2022•蚌埠三模）
【变式演练】
（2022·广东·高三专题练习）
