专题07 导数中的恒成立与能成立问题
【题型7】等价转化法
【典例分析】
(2022·福建·厦门高三阶段练习)
(2022·湖北模拟预测)
【变式演练】
(2022·全国·一模(理))
(2022·湖北·随州市高三阶段练习)
多变量恒成立问题处理策略:
“多变量含参恒成立”问题 ,例如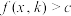 ,
,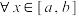 恒成立,可等价转化为
恒成立,可等价转化为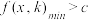 ,
,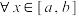 ,但参数 k 的“掺和”往往使函数的最值变得不确定,不可避免地要经分类讨论,进一步使整个解题过程显得繁琐不堪.其实,“含参恒成立”问题也可用“参变量分离” 的方法处理:将
,但参数 k 的“掺和”往往使函数的最值变得不确定,不可避免地要经分类讨论,进一步使整个解题过程显得繁琐不堪.其实,“含参恒成立”问题也可用“参变量分离” 的方法处理:将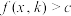 等价变形为
等价变形为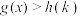 ,则等价于
,则等价于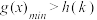 再解关于k的不等式即可,下面就多变量恒成立问题进行剖析.
再解关于k的不等式即可,下面就多变量恒成立问题进行剖析.
常见多变量恒成立(能成立)的转化:
①∀x1∈M,∃x2∈N,f(x1)>g(x2)⇔f(x)min>g(x)min
②∀x1∈M,∀x2∈N,f(x1)>g(x2)⇔f(x)min>g(x)max
③∃x1∈M,∃x2∈N,f(x1)>g(x2)⇔f(x)max>g(x)min
④∃x1∈M,∀x2∈N,f(x1)>g(x2)⇔f(x)max>g(x)max
⑤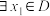 ,
, 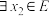 , 使得
, 使得 成立,则
成立,则 ;
;
⑥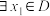 ,
, 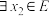 ,均使得
,均使得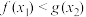 成立,则
成立,则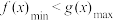 ;
;
⑦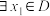 ,
,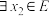 ,均使得
,均使得 成立,则
成立,则 .(其中
.(其中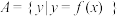 ,
,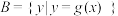 ).
).
【题型8】 双变量:转化为 f (x, k)min c( f (x, k)max c), x [a,b]类型
【典例分析】
(2022山西第四次模拟)
【变式演练】
(2022·四川·成都模拟(理))
(2022广东高三月考)
【题型9】双变量:以静制动,变量依次固定转化
【典例分析】
(2022·安徽高三阶段练习(理))
【变式演练】
(2023江西高三调研)
(2022广东高三模拟)
【题型10】双变量:分离后两侧同结构,可构造新函数
【典例分析】
(2022·湖北·仙桃高三阶段练习)
【变式演练】
(2022·福建福州·高三期中)
(2022山东高三一模)
(2022.山西高三模拟)
【题型11】双变量:分离后转化为两函数最值问题
【典例分析】
(2022吉林长春高三期中)
【变式演练】
(2022·河南洛阳·模拟预测(理))
(2022·北京·高三专题练习)
【题型12】双变量:齐次化或整体化构造
【典例分析】
(2022成都市高三模拟)
【变式演练】
(2022·河南·高三阶段练习(文))
(2022·广东·惠州市光正实验学校高三阶段练习)
(2022·广西北海·一模(理))
【题型13】多变量转化为单变量问题
【典例分析】
(2023·全国·高三专题练习)
【变式演练】
(2022·重庆·高二期末(理))
(2023山东省聊城市第二中学2019-2020学年高一上学期9月月考数学试题)
(2022湖南高三月考)


