第六篇 数论
专题1 数论中的特殊数
微点1 数论中的特殊数
【微点综述】
数论中的特殊数问题，是近年来各类考试的热门考点，这种题型给出一定规划下的定义(如“回文数”、“魔数”、“黑洞数”、对称数等)，要求找出符合这一规则的趣味自然数是哪些？有多少个？有什么性质？学生在解答这类题目时往往感到比较困难，其实，只要深刻理解了题目中新定义的含义，发现新定义的一些性质，并以此为依据，努力探索，准确推理，问题就可迎刃而解．本节我们介绍数论中的一些绚丽多姿的“趣味数”，以及它们在各类考试中的应用．
【典例刨析】
克鲁斯基说过“一个人对数学有了兴趁，就能专心致志，从而有力地应用和发展他的能力”，因此要使学生获得有价值的数学，不断提高数学修养，必须使学生对数学产生兴趣．先看一个例子：
例1．
【知识拓展】
1．回文数
定义：“回文”是指正读反读都能读通的句子，它是古今中外都有的一种修辞方式和文字游戏，如“我为人人，人人为我”等．在数学中也有这样一类数字有这样的特征，成为回文数．
设n是一任意自然数．若将n的各位数字反向排列所得自然数n1与n相等，则称n为一回文数．例如，若n=1234321，则称n为一回文数；但若n=1234567，则n不是回文数．
注意：1．偶数个的数字也有回文数1244212．小数没有回文数．
1.1 最简单的回文数
自然数中，最小的回文数是“0”.10以内的自然数都是回文数，如1，2，3，…，9．单个的回文数亦称“逆序数”，如11，101，121，…．
1.2 回文质数，
即两个质数互为回文数．如13与31，17与71，113与311，347与743等． 回文质数无规律可言，纯属巧合．
1.3 平方回数
定义：一个回文数，它同时还是某一个数的平方，这样的数字叫做平方回数．例如：121．
100以上至1000以内的平方回数只有3个，分别是：121，484，676．其中，121是11的平方.484是22的平方，同时还是121的4倍.676是26的平方，同时还是169的4倍．
1.4 回文数加法
（1）两个非回文数的和是回文数：
．
（2）一个回文数与一个非回文数的和是回文数：
．
（3）两个回文数的和仍为回文数：
．
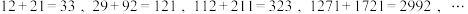1.5 回文数乘法
1.5.1 在乘法算式中，去掉等号和运算符号后成回文数
1．因数与积成回文数
，
．
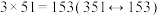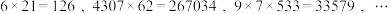2．两组数的积相等
．
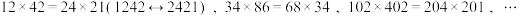1.5.2 几个回文数的积仍是回文数
，
．
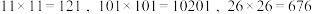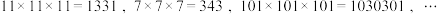1.5.3 相邻两数的积是一个回文数
，
，
．
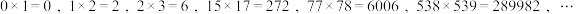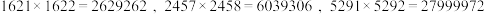以上为10000以内的相邻二数之积为回文数的自然数．
1.6 其它有趣的例子
四位的回文数有一个特点，就是它决不会是一个质数．设它为abba，那它等于a*1000+b*100+b*10+a，1001a+110b．能被11整除．六位的也一样，也能被11整除．
还有，人们借助电子计算机发现，在完全平方数、完全立方数中的回文数，其比例要比一般自然数中回文数所占的比例大得多．例如11^2=121，22^2=484，7^3=343，11^3=1331，11^4=14641……都是回文数．
1.7 回文数研究现状
人们迄今未能找到自然数（除0和1）的五次方，以及更高次幂的回文数．于是数学家们猜想：不存在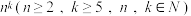
形式的回文数．
在电子计算器的实践中，还发现了一桩趣事：任何一个自然数与它的倒序数相加，所得的和再与和的倒序数相加，……如此反复进行下去，经过有限次步骤后，最后必定能得到一个回文数．
这也仅仅是个猜想，因为有些数并不“驯服”．比如说196这个数，按照上述变换规则重复了数十万次，仍未得到回文数．但是人们既不能肯定运算下去永远得不到回文数，也不知道需要再运算多少步才能最终得到回文数．
1.8 回文数算法
随意找一个十进制的数，把它倒过来成另一个数，再把这两个数相加，得一个和数，这是第一步；然后把这个和数倒过来，与原来的和数相加，又得到一个新的和数，这是第二步．照此方法，一步步接续往下算，直到出现一个“回文数”为n．例如：28+82=110，110+011=121，两步就得出了一个“回文数”．如果接着算下去，还会得到更多的“回文数”．这个过程称为“196算法”．
上面提到的196这个数，是第一个可能的“利克瑞尔数”，因而它受到了最多的关注．由于目前还不可能证明一个数永远不能形成“回文数”，所以“196和其他那些（看起来）不能形成回文数的数是利克瑞尔数”这一命题仅是猜想而非已获证明．能证明的仅是那些反例，即如果一个数最终能形成“回文数”，则它不是“利克瑞尔数”．
在电子计算机尚未问世的1938年，美国数学家莱默（D． Lehmer，1905-1991）计算到了第73步，得到了一个没有形成“回文数”的35位的和数．至今挑战此题的数学爱好者从没有间断过，并随着计算机科技的发展，不断有发烧友编写不同的程序对此题发起挑战．据笔者最新调查，领军人W．V．Landingham到2006年2月已经计算到了699万步，得到了一个2.89亿位以上的和数，之间的结果仍未出现“回文数”．
另外介绍一个关于达到“回文数”需要计算步数的世界记录．它是一个19位数字1，186，060，307，891，929，990，算出“回文数”，需要了261步．它是由Jason Doucette的算法及程序于2005年11月30日发现的．下表列举的是各位数字中，到达“回文数”花费步数最多的代表性数字．
2．素数（质数）
例2．
例3．（2023福建泉州石狮石光中学期中考试）
例4．
3．魔数
例5．
4．黑洞数
例6．（2023·河南南阳中学三模）
例7．
5．对称数
例8．
6．上升数
例9．
例10．
7．下滑数
例11．
例12．
【针对训练】
一、单选题：
二、多选题：
（2023山东菏泽郓城一期末考试）
三、填空题：
（2023云南·高三云南师大附中月考）
四、解答题：
（2021·浙江·高三竞赛）
（2018·全国·高三竞赛）
