一元函数的导数及其应用
一、单元学习目标
内容 | 目标要求 | 学科素养 |
导数的概念及其意义 | 1、通过求高台跳水运动员在具体时刻的瞬时速度，体会求瞬时速度的一般方法. 2、通过求曲线处某点处切线斜率的过程，体会求切线斜率的一般方法. 3、理解函数的平均变化率，瞬时变化率的概念． 4、经历由平均变化率到瞬时变化率的过程，体会导数的概念的实际背景． 5、了解导函数的概念，理解导数的几何意义． | 数学抽象 逻辑推理 数学运算 数学建模 |
导数的运算 | 1、能根据定义求函数y＝c，y＝x 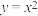 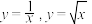，  的导数．2、掌握基本初等函数的导数公式，并能进行简单的应用 3、理解函数的和、差、积、商的求导法则． 4、能够综合运用导数公式和导数运算法则求函数的导数． 5、了解复合函数的概念． 6、理解复合函数的求导法则，并能求简单的复合函数的导数． | 数学抽象 逻辑推理 数学运算 直观想象 |
导数在研究函数中的应用 | 1、通过具体函数图象，发现函数的单调性与导数的正负之间的关系，体会数形结合思想，发展直观想象素养. 2、能根据函数导数的正负判断函数的单调性，体会算法思想，发展数学运算素养. 3、了解函数极值的概念，会从函数图象直观认识函数极值与导数的关系. 4、初步掌握求函数极值和最值的方法． 5、体会渗透在数学中的整体与局部的辩证关系． | 数学抽象 逻辑推理 数学运算 直观想象 |
二、单元知识架构
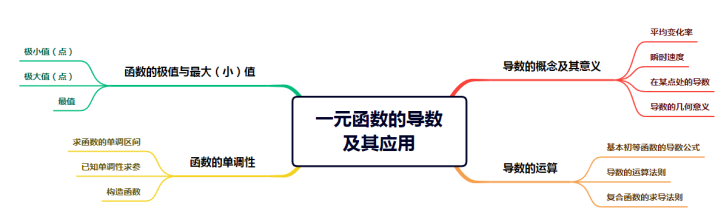
三、重点知识梳理
3. 导数的两条性质
（1）奇函数的导数是偶函数，偶函数的导数是奇函数.
（2）可导函数y＝f（x）的导数为f′（x），若f′（x）为增函数，则f（x）的图象是下凹的；反之，若f′（x）为减函数，则f（x）的图象是上凸的.
4. 几类重要切线方程
（1）y＝x－1是曲线y＝lnx的切线，y＝x是曲线y＝ln（x＋1）的切线，…，y＝x＋n是曲线y＝ln（x＋n＋1）的切线，如图1.
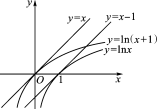
图1 图2
（2）y＝x＋1与y＝ex是曲线y＝ex的切线，如图2.
（3）y＝x是曲线y＝sinx与y＝tanx的切线，如图3.
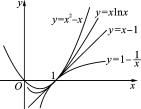
图3 图4
（4）y＝x－1是曲线y＝x2－x，y＝xlnx及y＝1－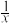
的切线，如图4. 由以上切线方程又可得重要不等式，如lnx≤x－1，x＋1≤ex等. 6. 利用导数判断函数f（x）单调性的步骤
第1步，确定函数的定义域；
第2步，求出导数f′（x）的零点；
第3步，用f′（x）的零点将f（x）的定义域划分为若干个区间，列表给出f′（x）在各个区间上的正负，由此得出函数y＝f（x）在定义域内的单调性.
8. 构造函数解抽象不等式
（1）对于不等式f′（x）>k（k≠0），构造函数g（x）＝f（x）－kx＋b.
（2）对于不等式xf′（x）＋f（x）>0，构造函数g（x）＝xf（x）；对于不等式xf′（x）－f（x）>0，构造函数g（x）＝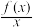
（x≠0）. （3）对于不等式xf′（x）＋nf（x）>0，构造函数g（x）＝xnf（x）；对于不等式xf′（x）－nf（x）>0，构造函数g（x）＝
（x≠0）. （4）对于不等式f′（x）＋f（x）>0，构造函数g（x）＝exf（x）；对于不等式f′（x）－f（x）>0，构造函数g（x）＝
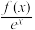. （5）对于不等式f′（x）sinx＋f（x）cosx>0（或f（x）＋f′（x）tanx>0），构造函数g（x）＝f（x）sinx；对于不等式f′（x）cosx－f（x）sinx>0（或f′（x）－f（x）tanx>0），构造函数g（x）＝f（x）cosx.
11. 三次函数的图象、单调性、极值
设三次函数f（x）＝ax3＋bx2＋cx＋d（a≠0），则f′（x）＝3ax2＋2bx＋c，记Δ＝4b2－12ac＝4（b2－3ac），并设x1，x2是方程f′（x）＝0的根，且x1<x2.
（1）a>0
Δ>0 | Δ≤0 | |
图 象 |  |  |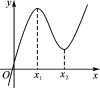
单调性 | 在（－∞，x1），（x2，＋∞）上单调递增；在（x1，x2）上单调递减 | 在R上是增函数 |
极值点 个数 | 2 | 0 |
（2）a<0
Δ>0 | Δ≤0 | |
图 象 |  |  |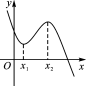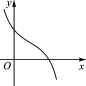
单调性 | 在（x1，x2）上单调递增；在（－∞，x1），（x2，＋∞）上单调递减 | 在R上是减函数 |
极值点 个数 | 2 | 0 |
