三角函数
一、单元学习目标
内容 | 目标要求 | |
任意角和弧度制 | 1、了解任意角的概念; 2、掌握正角、负角、零角及象限角的定义,理解任意角的概念; 3、掌握终边相同的角的表示方法; 4、会判断角所在的象限; 5、理解角集与实数集的一一对应,熟练掌握角度制与弧度制间的互相转化; 6、能灵活运用弧长公式、扇形面积公式解决问题; 7、找出弧度与角度换算的方法,领悟从特殊到一般的思想方法. | 数学抽象 逻辑推理 数学运算 直观想象 |
三角函数的概念 | 1、借助单位圆理解任意角三角函数(正弦、余弦、正切)的定义; 2、掌握任意角三角函数(正弦、余弦、正切)在各象限的符号; 3、掌握公式一并会应用; 4、理解并掌握同角三角函数基本关系式的推导及应用; 5、会利用同角三角函数的基本关系式进行化简、求值与恒等式证明. | 数学抽象 逻辑推理 数学运算 直观想象 |
诱导公式 | 1、借助单位圆,推导出正弦、余弦第二、三、四、五、六组的诱导公式,能正确运用诱导公式将任意角的三角函数化为锐角的三角函数,并解决有关三角函数求值、化简和恒等式证明问题; 2、通过公式的应用,了解未知到已知、复杂到简单的转化过程,培养学生的化归思想,以及信息加工能力、运算推理能力、分析问题和解决问题的能力. | 数学抽象 逻辑推理 数学运算 |
三角函数的图象和性质 | 1、掌握“五点法”画正弦曲线和余弦曲线的步骤和方法,能用“五点法”作出简单的正弦、余弦曲线; 2、理解正弦曲线与余弦曲线之间的联系; 3、了解周期函数与最小正周期的意义; 4、了解三角函数的周期性和奇偶性; 5、会利用周期性定义和诱导公式求简单三角函数的周期; 6、借助图象直观理解正、余弦函数在[0,2π]上的性质(单调性、最值、图象与轴的交点等); 7、能利用性质解决一些简单问题; 8、理解并掌握正切函数的周期性、定义域、值域、奇偶性和单调性,并能够应用正切函数的图象和性质解决相关问题; 9、会利用正切线及正切函数的性质作正切函数的图象; 10、通过正切函数图像与性质的探究,培养学生数形结合和类比的思想方法. | 数学抽象 逻辑推理 直观想象 数学运算 数学建模 |
三角恒等变换 | 1、了解两角差的余弦公式的推导过程,体会单位圆上点的坐标的表示方法; 2、会用两角差的余弦公式进行简单的三角函数的求值、化简、计算等; 3、熟悉两角差的余弦公式的灵活运用,了解公式的正用、逆用以及角的变换的常用方法; 4、掌握由两角差的余弦公式推导出两角和的余弦公式及两角和与差的正弦、正切公式; 5、熟悉两角和与差的正弦、余弦、正切公式的灵活运用,了解公式的正用、逆用以及角的变换的常用方法; 6、能够利用两角和的正弦、余弦、正切公式推导二倍角公式,并能应用; 7、掌握二倍角公式及变形公式,能灵活运用二倍角公式解决有关的化简、求值、证明问题; 8、利用二倍角的变形公式推导半角的正弦、余弦、正切公式; 9、通过三角恒等变形将形如asin x+bcos x的函数转化为y=Asin(x+φ)的函数; 10、灵活利用公式,通过三角恒等变形,解决函数的最值、周期、单调性等问题. | 数学抽象 逻辑推理 数学运算 数学建模 |
函数 | 1、结合实例,探究对函数图象的影响; 2、结合实例,探究对函数周期的影响,加深对周期函数概念的理解; 3、结合实例,探究对函数图象的影响; 4、会用“五点法”画y=Asin(ωx+φ)的图象; 5、会根据函数图象求对应的函数解析式. | 数学抽象 逻辑推理 数学运算 直观想象 |
三角函数的应用 | 1、了解三角函数是描述周期变化现象的重要函数模型,并会用三角函数模型解决一些简单的实际问题; 2、会将实际问题抽象为三角函数模型. | 数学抽象 数学运算 数学建模 |
二、单元知识架构
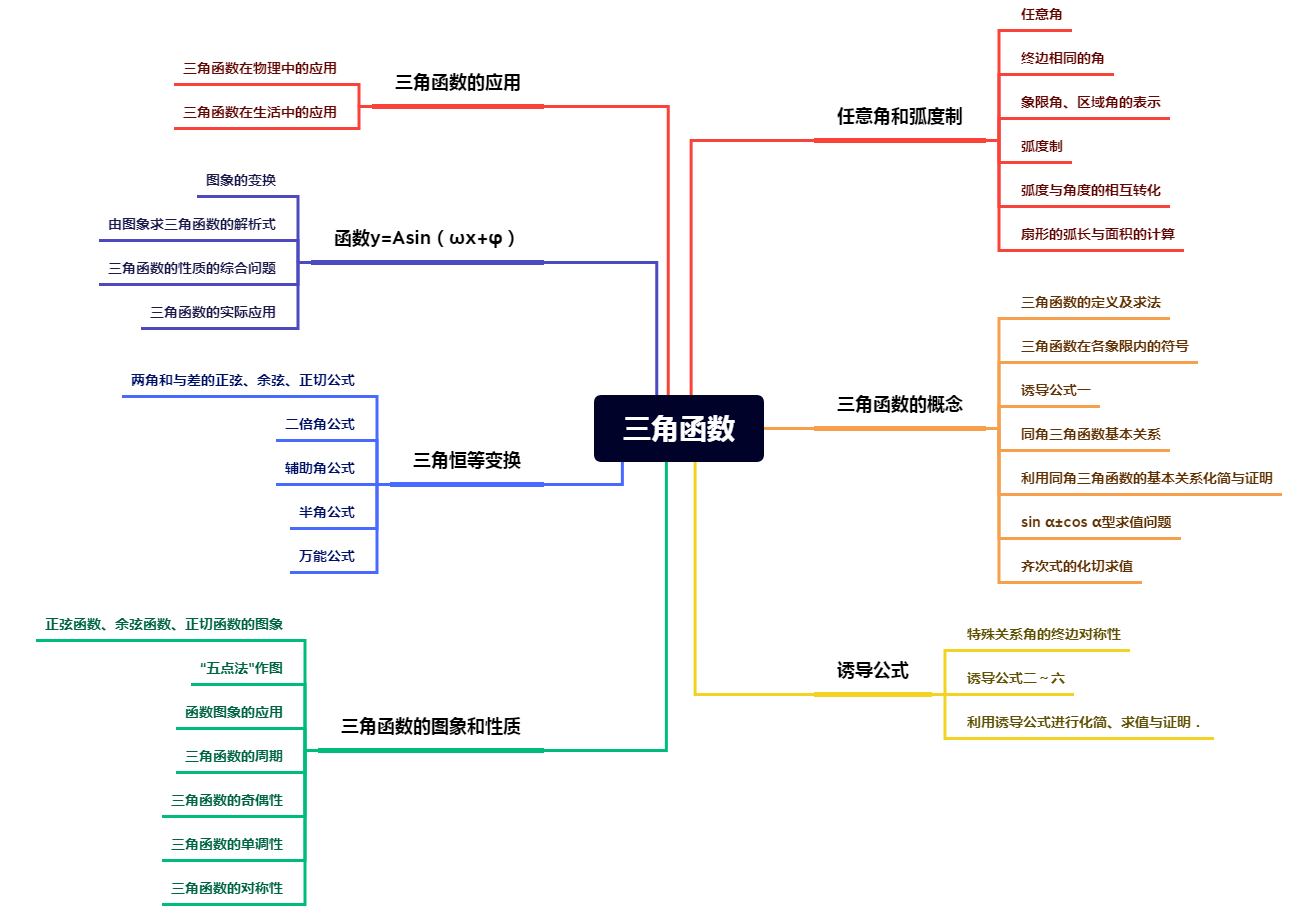
三、重点知识梳理
(一)任意角和弧度制
(二)三角函数的概念
(三)诱导公式
(四)三角函数的图象和性质
(五)三角恒等变换
(七)函数
(八)三角函数的应用
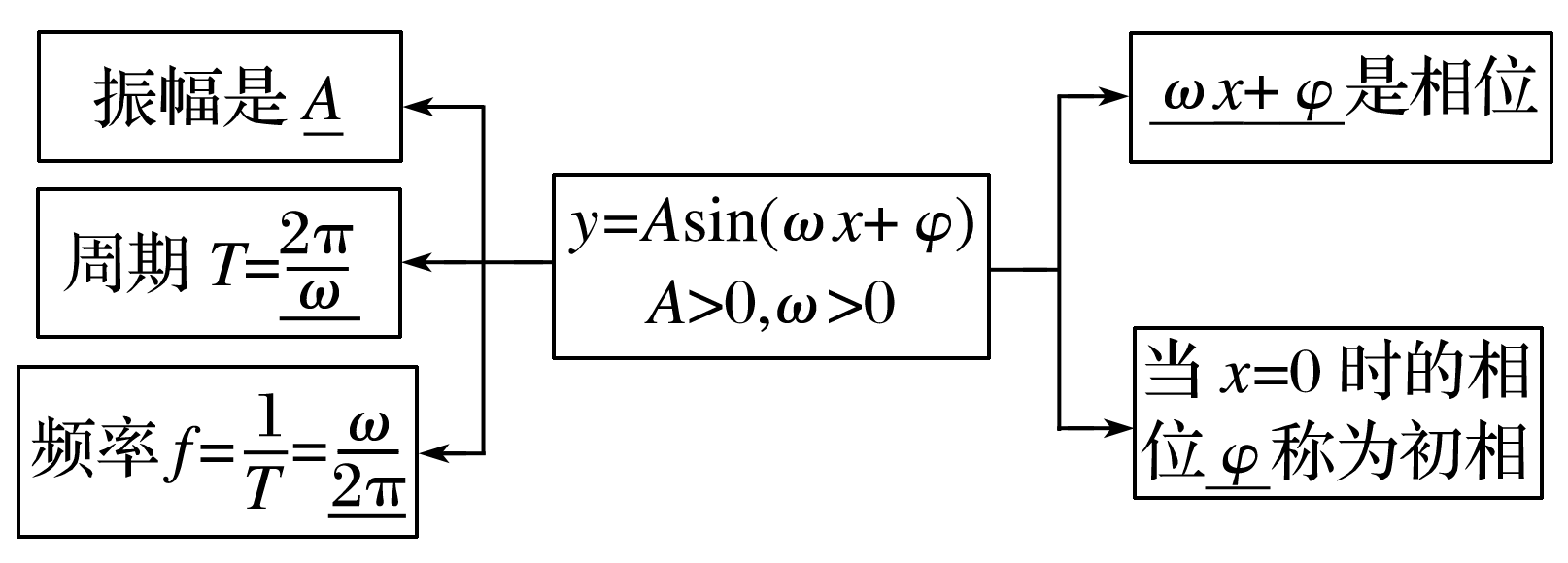
23.函数y=Asin(ωx+φ),A>0,ω>0中参数的物理意义

打开组卷App 获取专属积分,充值下载直接抵现

