2023年高考数学一轮复习讲练测·第01讲 基本立体图形、简单几何体的表面积与体积 (精讲）-1

第01讲 基本立体图形、简单几何体的表面积与体积 (精讲）

目录

第一部分：知识点精准记忆

第二部分：课前自我评估测试

第三部分：典型例题剖析

题型一：基本立体图形

角度1：结构特征

角度2：直观图

角度3：展开图

题型二：空间几何体的表面积与体积

角度1：表面积和侧面积

角度2：体积

角度3：蚂蚁爬行最短问题

题型三：空间几何体的外接球

角度1：补形法

角度2：对棱相等型

角度3：借助三角形外心确定球心

题型四：空间几何体的内切球

第四部分：高考真题感悟

知识点一：空间几何体的结构特征

1、多面体的结构特征

1.1棱柱

（1）棱柱的定义

定义：一般地，有两个面互相平行 ，其余各面都是四边形，并且相邻两个四边形的公共边都互相平行 ，由这些面所围成的多面体叫做棱柱

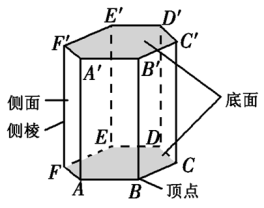
底面(底)：两个互相平行的面

侧面：其余各面

侧棱：相邻侧面的公共边

顶点：侧面与底面的公共顶点

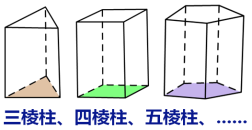
（2）棱柱的图形

（3）棱柱的分类及表示

①按棱柱底面边数分类:

②按棱柱侧棱与底面位置关系分类:

③直棱柱：侧棱垂直于底面的棱柱

斜棱柱：侧棱不垂直于底面的棱柱

正棱柱：底面是正多边形的直棱柱

平行六面体：底面是平行四边形的四棱柱

表示法：用各顶点字母表示棱柱，如图棱柱$ABCDEF-A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }{E}^{\prime }{F}^{\prime }$

1.2棱锥

（1）棱锥的定义

定义：有一面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的多面体叫做棱锥

底面：多边形面

侧面：有公共顶点的各三角形面

侧棱：相邻侧面的公共边

顶点：各侧面的公共顶点

（2）棱锥的图形

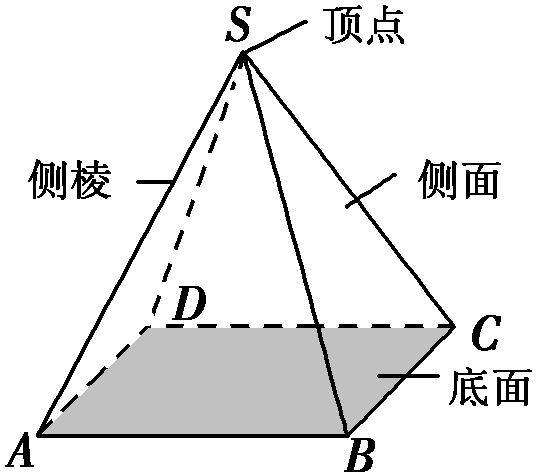
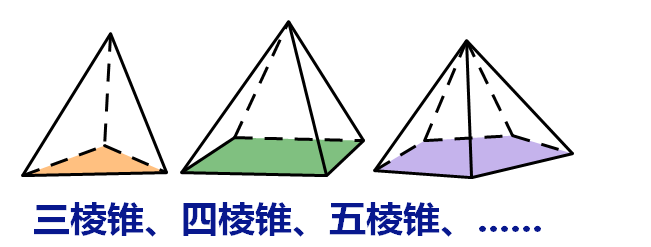
（3）棱锥的分类及表示

按照棱锥的底面多边形的边数，棱锥可分为： 三棱锥、四棱锥、五棱锥……

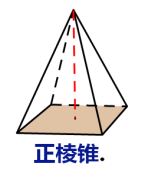
特别地，三棱锥又叫四面体，底面是正多边形，且顶点与底面中心的连线垂直于底面的棱锥叫做正棱锥

表示法：棱锥也用顶点和底面各顶点字母表示，如图棱锥$S-ABCD$

1.3棱台

（1）棱台的定义

定义：用一个平行于棱锥底面的平面去截棱锥，我们把底面和截面之间的那部分多面体叫做棱台

上底面：原棱锥的截面

下底面：原棱锥的底面

侧面：除上下底面以外的面

侧棱：相邻侧面的公共边

顶点：侧面与上(下)底面的公共顶点

（2）棱台的图形

（3）棱台的分类及表示

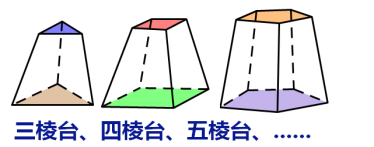
由三棱锥、四棱锥、五棱锥……截得的棱台分别叫做三棱台、四棱台、五棱台……

用各顶点字母表示棱柱，如棱台$ABCD-A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$

2、旋转体的结构特征

2.1圆柱

（1）圆柱的定义

以矩形的一边所在的直线为旋转轴，其余三边旋转形成的面所围成的旋转体

圆柱的轴：旋转轴

圆柱的底面：垂直于轴的边旋转而成的圆面

圆柱的侧面：平行于轴的边旋转而成的曲面

圆柱侧面的母线：无论旋转到什么位置，平行于轴的边

（2）圆柱的图形

（3）圆柱的表示

圆柱用表示它的轴的字母表示，如图，圆柱$O{O}^{\prime }$

2.2圆锥

（1）圆锥的定义

以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转一周形成的面所围成的旋转体

轴：旋转轴叫做圆锥的轴

底面：垂直于轴的边旋转而成的圆面

侧面：直角三角形的斜边旋转而成的曲面

母线：无论旋转到什么位置，不垂直于轴的边

锥体：棱锥和圆锥统称为锥体

（2）圆锥的图形

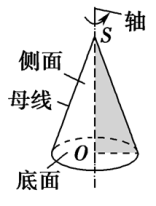
（3）圆锥的表示

用表示它的轴的字母表示，如图，圆锥$SO$

2.3圆台

（1）圆台的定义

用平行于圆锥底面的平面去截圆锥，底面和截面之间的部分叫做圆台

轴：圆锥的轴

底面：圆锥的底面和截面

侧面：圆锥的侧面在底面与截面之间的部分

母线：圆锥的母线在底面与截面之间的部分

台体：棱台和圆台统称为台体

（2）圆台的图形

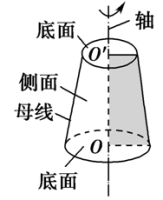
（3）圆台的表示

用表示它的轴的字母表示，如图，圆台$O{O}^{\prime }$

2.4球

球的表面积和体积

（1）球的表面积：$S\text{=}4\pi R^2$

（2）球的体积:$V=\frac{4}{3}\pi R^3$

知识点二：直观图

1、空间几何体的直观图的绘制方法

（1）画轴. 在平面图形中取互相垂直的$x$轴和$y$轴，两轴相交于点$O$， 画直观图时，把它们分别画成对应的$x^{\prime }$轴与$y^{\prime }$轴，两轴交于点$O^{\prime }$， 且使$\angle x^{\prime }{O}^{\prime }{y}^{\prime }={45}^{\circ }$”(或${135}^o$）， 它们确定的平面表示水平面；

（2）画底面. 已知图形中，平行于$x$轴$y$轴或$z$轴的线段，在直观图中分别画成平行于$x^{\prime }$轴、$y^{\prime }$轴或$z^{\prime }$轴的线段；

（3）画侧棱. 已知图形中平行于$x$轴或$z$轴的线段，在直观图中保持长度不变，平行于$y$轴的线段，长度变为原来的一半；

（4）成图. 连线成图以后，擦去作为辅助线的坐标轴，就得到了空间图形的直观图.

简记为：①画轴；②画底面；③画侧棱；④成图.

2、斜二测画法保留了原图形中的三个性质

①平行性不变，即在原图中平行的线在直观图中仍然平行；②共点性不变，即在原图中相交的直线仍然相交；③平行于x，z轴的长度不变．

知识点三：柱、锥、台、球的表面积和体积

知识点四：圆柱、圆锥、圆台的侧面展开图及侧面积公式

几何体	圆柱	圆锥	圆台
图示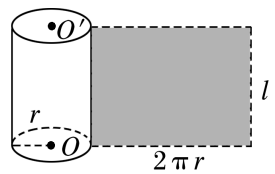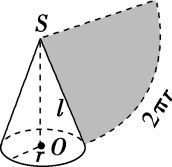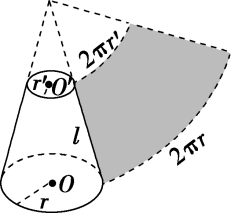
侧面积公式	$S_{\mathrm{侧}}\text{=}2\pi rl$	$S_{\mathrm{侧}}\text{=}\pi rl$	$S_{\mathrm{侧}}\text{=}\pi \mathrm{（}{r}^{\prime }\text{+}r\mathrm{）}l$

常用结论

1.球的截面的性质

(1)球的截面是圆面，且球心和截面(不过球心)圆心的连线垂直于截面;

(2)球心到截面的距离$d$与球的半径$R$及截面的半径$r$的关系为$r=\sqrt{R^2-d^2}$

（2022·河南商丘·高一期末）

（2022·广东珠海·高一期末）

（2022·黑龙江·铁人中学高一期末）

（2022·山东聊城·高一期末）

（2022·上海奉贤区致远高级中学高一期末）

（2022·贵州黔西·高二期末（理））

题型一：基本立体图形

角度1：结构特征

典型例题

（2022·江西上饶·高一期末）

（2022·辽宁·东港市第二中学高一阶段练习）

角度2：直观图

典型例题

（2022·广东广州·高一期末）

（2022·广西贵港·高一期末）

角度3：展开图

典型例题

（2022·浙江·温州中学高二期末）

（2022·广东韶关·高二期末）

题型归类练

（2022·山西吕梁·高一期末）

（2022·广西梧州·高一期末）

（2022·重庆·高一阶段练习）

（2022·全国·高一专题练习）

（2022·云南楚雄·高一期末）

（2022·四川·成都七中高二阶段练习（理））