专题36 切线与切点弦问题
【方法技巧与总结】
1、点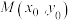 在圆
在圆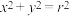 上,过点
上,过点 作圆的切线方程为
作圆的切线方程为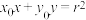 .
.
2、点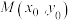 在圆
在圆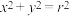 外,过点
外,过点 作圆的两条切线,切点分别为
作圆的两条切线,切点分别为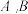 ,则切点弦
,则切点弦 的直线方程为
的直线方程为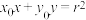 .
.
3、点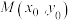 在圆
在圆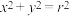 内,过点
内,过点 作圆的弦
作圆的弦 (不过圆心),分别过
(不过圆心),分别过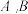 作圆的切线,则两条切线的交点
作圆的切线,则两条切线的交点 的轨迹方程为直线
的轨迹方程为直线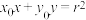 .
.
4、点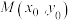 在圆
在圆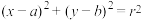 上,过点
上,过点 作圆的切线方程为
作圆的切线方程为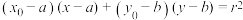 .
.
5、点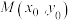 在圆
在圆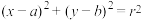 外,过点
外,过点 作圆的两条切线,切点分别为
作圆的两条切线,切点分别为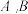 ,则切点弦
,则切点弦 的直线方程为
的直线方程为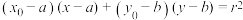 .
.
6、点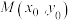 在圆
在圆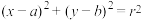 内,过点
内,过点 作圆的弦
作圆的弦 (不过圆心),分别过
(不过圆心),分别过 作圆的切线,则两条切线的交点
作圆的切线,则两条切线的交点 的轨迹方程为
的轨迹方程为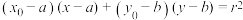 .
.
7、点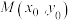 在椭圆
在椭圆
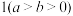 上,过点
上,过点 作椭圆的切线方程为
作椭圆的切线方程为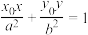 .
.
8、点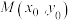 在椭圆
在椭圆
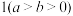 外,过点
外,过点 作椭圆的两条切线,切点分别为
作椭圆的两条切线,切点分别为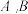 ,则切点弦
,则切点弦 的直线方程为
的直线方程为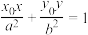 .
.
9、点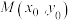 在椭圆
在椭圆
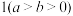 内,过点
内,过点 作椭圆的弦
作椭圆的弦 (不过椭圆中心),分别过
(不过椭圆中心),分别过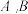 作椭圆的切线,则两条切线的交点
作椭圆的切线,则两条切线的交点 的轨迹方程为直线
的轨迹方程为直线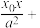
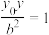 .
.
10、点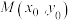 在双曲线
在双曲线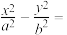
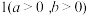 上,过点
上,过点 作双曲线的切线方程为
作双曲线的切线方程为 .
.
11、点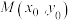 在双曲线
在双曲线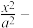
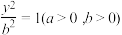 外,过点
外,过点 作双曲线的两条切线,切点分别为
作双曲线的两条切线,切点分别为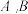 ,则切点弦
,则切点弦 的直线方程为
的直线方程为 .
.
12、点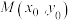 在双曲线
在双曲线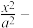
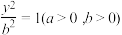 内,过点
内,过点 作双曲线的弦
作双曲线的弦 (不过双曲线中心),分别过
(不过双曲线中心),分别过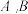 作双曲线的切线,则两条切线的交点
作双曲线的切线,则两条切线的交点 的轨迹方程为直线
的轨迹方程为直线 .
.
13、点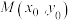 在抛物线
在抛物线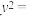
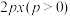 上,过点
上,过点 作抛物线的切线方程为
作抛物线的切线方程为 .
.
14、点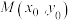 在抛物线
在抛物线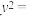
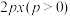 外,过点
外,过点 作抛物线的两条切线,切点分别为
作抛物线的两条切线,切点分别为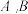 ,则切点弦
,则切点弦 的直线方程为
的直线方程为 .
.
15、点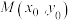 在抛物线
在抛物线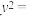
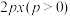 内,过点
内,过点 作抛物线的弦
作抛物线的弦 ,分别过
,分别过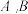 作抛物线的切线,则两条切线的交点
作抛物线的切线,则两条切线的交点 的轨迹方程为直线
的轨迹方程为直线 .
.
【典例例题】
题型一:切线问题
变式1
变式2.
题型二:切点弦过定点问题
题型三:利用切点弦结论解决定值问题
题型四:利用切点弦结论解决最值问题
题型五:利用切点弦结论解决范围问题
变式3.
变式4.
变式5.
变式6.
变式7.

打开组卷App 获取专属积分,充值下载直接抵现

