解答题-证明题 0.65 引用1 组卷187
新定义:我们把两个面积相等但不全等的三角形叫做偏等积三角形.
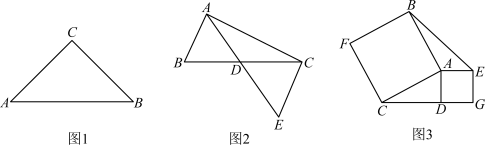
(1)初步尝试:如图1,已知等腰直角△ABC,∠ACB=90°,AC=BC=5,P为AC上一点,当AP=_____时,△ABP与△CBP为偏等积三角形;
(2)理解运用:如图2,△ABD与△ACD为偏等积三角形,若AB=2,AC=5,且线段AD的长度为正整数,过点C作CE//AB,交AD的延长线于点E,求AE的长;
(3)综合应用:如图3,已知△ACD为直角三角形,∠ADC=90°,分别以AC,AD为边向外作正方形ACFB和正方形ADGE,连接BE,求证:△ACD与△ABE为偏等积三角形.

(1)初步尝试:如图1,已知等腰直角△ABC,∠ACB=90°,AC=BC=5,P为AC上一点,当AP=_____时,△ABP与△CBP为偏等积三角形;
(2)理解运用:如图2,△ABD与△ACD为偏等积三角形,若AB=2,AC=5,且线段AD的长度为正整数,过点C作CE//AB,交AD的延长线于点E,求AE的长;
(3)综合应用:如图3,已知△ACD为直角三角形,∠ADC=90°,分别以AC,AD为边向外作正方形ACFB和正方形ADGE,连接BE,求证:△ACD与△ABE为偏等积三角形.
22-23八年级上·湖南长沙·开学考试


