解答题-证明题 0.4 引用6 组卷1305
若一个三角形的最大内角小于120°,则在其内部有一点所对三角形三边的张角均为120°,此时该点叫做这个三角形的费马点.如图1,当△ABC三个内角均小于120°时,费马点P在△ABC内部,此时 ,
, 的值最小.
的值最小.
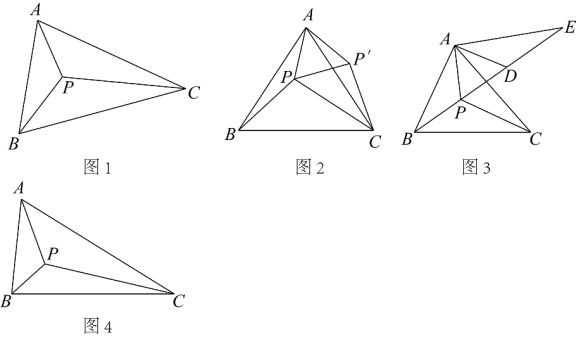
(1)如图2,等边三角形ABC内有一点P,若点P到顶点A,B,C的距离分别为3,4,5,求 的度数.为了解决本题,小林利用“转化”思想,将△ABP绕顶点A旋转到
的度数.为了解决本题,小林利用“转化”思想,将△ABP绕顶点A旋转到 处,连接
处,连接 ,此时
,此时 ,这样就可以通过旋转变换,将三条线段PA,PB,PC转化到一个三角形中,从而求出
,这样就可以通过旋转变换,将三条线段PA,PB,PC转化到一个三角形中,从而求出 ______.
______.
(2)如图3,在图1的基础上延长BP,在射线BP上取点D,E,连接AE,AD.使 ,
, ,求证:
,求证: .
.
(3)如图4,在直角三角形ABC中 , ,
, ,
, ,点P为直角三角形ABC的费马点,连接AP,BP,CP,请直接写出
,点P为直角三角形ABC的费马点,连接AP,BP,CP,请直接写出 的值.
的值.

(1)如图2,等边三角形ABC内有一点P,若点P到顶点A,B,C的距离分别为3,4,5,求
(2)如图3,在图1的基础上延长BP,在射线BP上取点D,E,连接AE,AD.使
(3)如图4,在直角三角形ABC中 ,
2022·山东德州·一模


