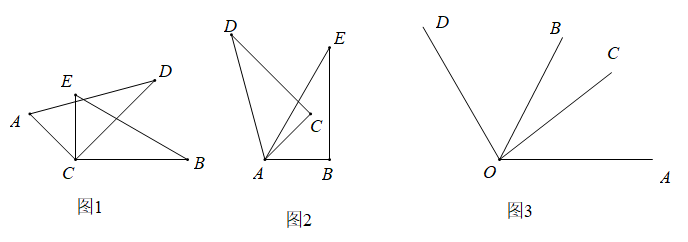
（1）如图1，将一副直角三角尺的直角顶点C叠放在一起，经探究发现∠ACB与∠DCE的和不变．证明过程如下：
由题可知∠BCE＝∠ACD＝90°
∴∠ACB＝          +∠BCD．
∴∠ACB＝90°+∠BCD．
∴∠ACB+∠DCE
＝90°+∠BCD+∠DCE
＝90°+∠BCE
∵∠BCE＝90°，
∴∠ACB+∠DCE＝          ．
（2）如图2，若将两个含有60°的三角尺叠放在一起，使60°锐角的顶点A重合，则∠DAB与∠CAE有怎样的数量关系，并说明理由；
（3）如图3，已知∠AOB＝α，∠COD＝β（α，β都是锐角），若把它们的顶点O重合在一起，请直接写出∠AOD与∠BOC的数量关系．