古希腊七贤之一，著名哲学家泰勒斯（Thales，公元前6世纪）最早从拼图实践中发现了“三角形内角和等于180°”，但这种发现完全是经验性的，泰勒斯并没有给出严格的证明．之后古希腊数学家毕达哥拉斯、欧几里得、普罗科拉斯等相继给出了基于平行线性质的不同的证明．其中欧几里得利用辅助平行线和延长线，通过一组同位角和内错角证明了该定理．
（1）请同学们帮助欧几里得将证明过程补充完整．（在横线上填写相应的几何语言，在括号内填写相应的推理依据）．
已知：如图，在△ABC中，求证：∠A+∠B+∠BCA＝180°．

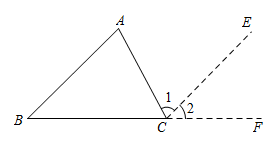
解：延长线段BC至点F，并过点C作CE//AB．
因为CE//AB（已作），
所以∠A＝       （                                             ），
∠B ＝         （                                               ）．   
因为 ∠ACB+∠1+∠2＝180°（平角定义），
所以∠A+∠B+∠ACB＝180°（                      ）．
（2）请你再思考另外一种证明三角形内角和定理的方法并加以证明．（此题不用写推理依据即可）．