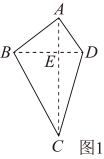
定义：我们把对角线互相垂直的四边形叫做垂美四边形．
   　   　   　   
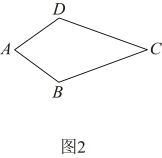
（1）概念理解：如图2，在四边形ABCD中，AB=AD，CB=CD，那么四边形ABCD是垂美四边形吗？请说明理由．
（2）性质探究：
①如图1，垂美四边形ABCD两组对边AB、CD与BC、AD之间有怎样的数量关系？写出你的猜想，并给出证明．
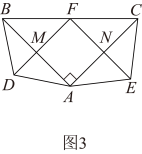
②如图3，在Rt△ABC中，点F为斜边BC的中点，分别以AB，AC为底边，在外部作等腰三角形ABD和等腰三角形ACE，连接FD，FE，分别交AB，AC于点M，N．试猜想四边形FMAN的形状，并说明理由；
（3）问题解决：
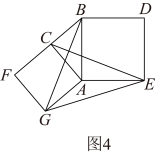
如图4，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE、BG，GE，已知AC=2，AB=5．求GE的长度．