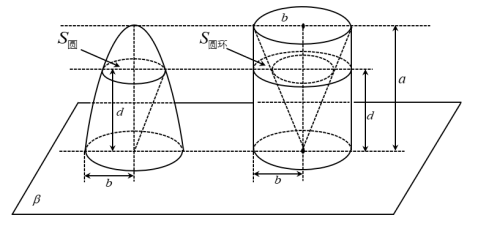
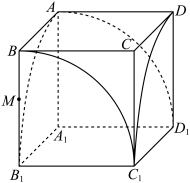
南北朝时期的伟大科学家祖暅，于五世纪末提出了体积计算原理，即祖暅原理：“夫叠棋成立积，缘幂势既同，则积不容异”.意思是：夹在两个平行平面之间的两个几何体，被平行于这两个平面的任意平面所截，如果截得的两个截面的面积总相等，那么，这两个几何体的体积相等.其最著名之处是解决了“牟合方盖”的体积问题.如图所示，正方体，棱长为.

(1)求图中四分之一圆柱体的体积；
(2)在图中画出四分之一圆柱体与四分之一圆柱体的一条交线（不要求说明理由）；
(3)四分之一圆柱体与四分之一圆柱体公共部分是八分之一个“牟合方盖”.点在棱上，设.过点作一个与正方体底面平行的平面，求该截面位于八分之一“牟合方盖”内部分的面积；
(4)如果令，求出八分之一“牟合方盖”的体积.