解答题-证明题 0.85 引用3 组卷293
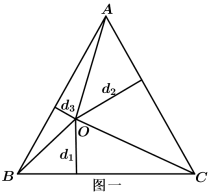
如图一,在平面几何中,有如下命题“正三角形 的高为h,O是
的高为h,O是 内任意一点,则O到三边的距离的和为定值h,当O是
内任意一点,则O到三边的距离的和为定值h,当O是 的中心时,O到各边的距离均为
的中心时,O到各边的距离均为 ”.
”.
证明如下:设正三角形 边长为a,高h,O到三边的距离分别
边长为a,高h,O到三边的距离分别
则: ,即:
,即:

化简得,
若O是 中心,则
中心,则
即:正三角形中心到各边的距离均为
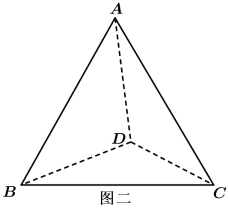
类比此命题及证明方法,在立体几何中,请写出高为h的正四面体 (图二)相应的命题,并证明你的结论.
(图二)相应的命题,并证明你的结论.
证明如下:设正三角形
则:
化简得,
若O是
即:正三角形中心到各边的距离均为

类比此命题及证明方法,在立体几何中,请写出高为h的正四面体

20-21高一下·浙江·期末


